Нахождение лучшей точки компромисса на кривой
Скажем, у меня были некоторые данные, для которых я хочу поместить на него параметризованную модель. Моя цель - найти наилучшее значение для этого параметра модели.
Я делаю выбор модели с использованием критерия типа AIC/BIC/MDL, который вознаграждает модели с низкой ошибкой, но также наказывает модели с высокой сложностью (мы ищем простейшее, но наиболее убедительное объяснение этих данных, так сказать, a la Occam бритва).
Следуя приведенному выше, это пример того, что я получаю по трем различным критериям (два должны быть сведены к минимуму, а один - максимальным):
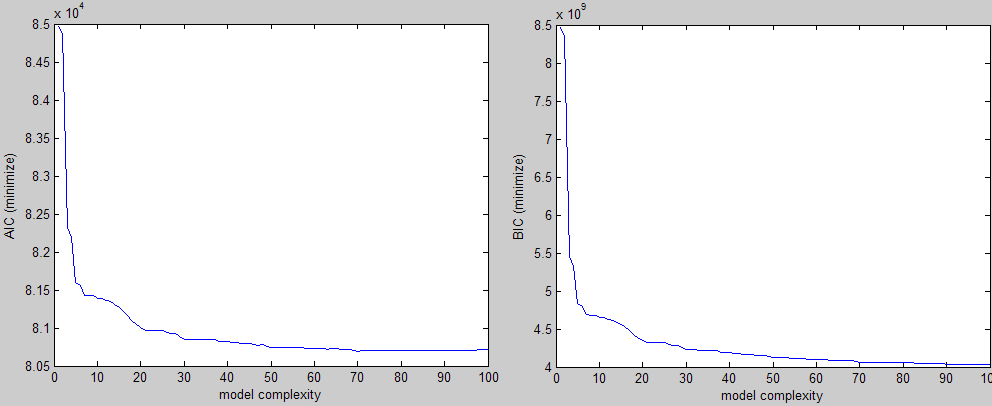
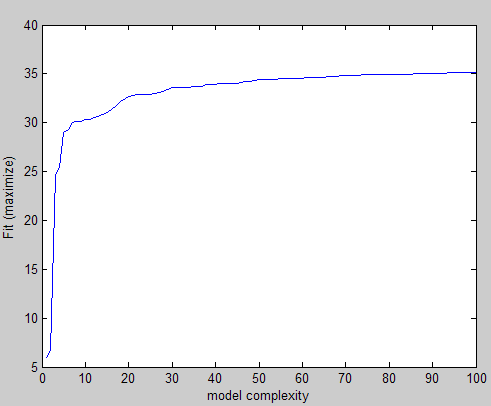
Визуально вы можете легко увидеть форму локтя, и вы выберете значение параметра в этом регионе. Проблема в том, что я делаю это для большого количества экспериментов, и мне нужен способ найти это значение без вмешательства.
Моя первая интуиция заключалась в том, чтобы попытаться нарисовать линию под углом 45 градусов от угла и продолжать перемещать ее, пока она не пересечет кривую, но это легче сказать, чем сделать :) Также он может пропустить интересующую область, если кривая несколько искажена.
Любые мысли о том, как реализовать это, или о лучших идеях?
Здесь образцы должны были воспроизвести один из приведенных выше графиков:
curve = [8.4663 8.3457 5.4507 5.3275 4.8305 4.7895 4.6889 4.6833 4.6819 4.6542 4.6501 4.6287 4.6162 4.585 4.5535 4.5134 4.474 4.4089 4.3797 4.3494 4.3268 4.3218 4.3206 4.3206 4.3203 4.2975 4.2864 4.2821 4.2544 4.2288 4.2281 4.2265 4.2226 4.2206 4.2146 4.2144 4.2114 4.1923 4.19 4.1894 4.1785 4.178 4.1694 4.1694 4.1694 4.1556 4.1498 4.1498 4.1357 4.1222 4.1222 4.1217 4.1192 4.1178 4.1139 4.1135 4.1125 4.1035 4.1025 4.1023 4.0971 4.0969 4.0915 4.0915 4.0914 4.0836 4.0804 4.0803 4.0722 4.065 4.065 4.0649 4.0644 4.0637 4.0616 4.0616 4.061 4.0572 4.0563 4.056 4.0545 4.0545 4.0522 4.0519 4.0514 4.0484 4.0467 4.0463 4.0422 4.0392 4.0388 4.0385 4.0385 4.0383 4.038 4.0379 4.0375 4.0364 4.0353 4.0344];
plot(1:100, curve)
РЕДАКТИРОВАТЬ
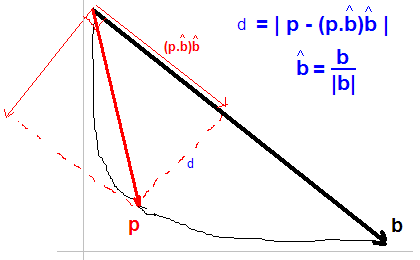
Я принял решение, данное Йонасом. В принципе, для каждой точки p на кривой найдем ту, которая имеет максимальное расстояние d заданное:
-
0Я собирался сказать, нарисовать линию 45 градусов тоже: \mpen
-
0Насколько вы ожидаете, что ваши графики будут отклоняться от общих форм в приведенных выше примерах? Другими словами, ожидаете ли вы, что «колено» графика всегда будет находиться в одном и том же углу графика?gnovice
10 ответов
Быстрый способ нахождения локтя - провести линию от первой до последней точки кривой, а затем найти точку данных, которая находится дальше всего от этой линии.
Это, конечно, несколько зависит от количества точек, которые у вас есть в плоской части линии, но если вы каждый раз проверяете одинаковое количество параметров, оно должно получиться достаточно хорошо.
curve = [8.4663 8.3457 5.4507 5.3275 4.8305 4.7895 4.6889 4.6833 4.6819 4.6542 4.6501 4.6287 4.6162 4.585 4.5535 4.5134 4.474 4.4089 4.3797 4.3494 4.3268 4.3218 4.3206 4.3206 4.3203 4.2975 4.2864 4.2821 4.2544 4.2288 4.2281 4.2265 4.2226 4.2206 4.2146 4.2144 4.2114 4.1923 4.19 4.1894 4.1785 4.178 4.1694 4.1694 4.1694 4.1556 4.1498 4.1498 4.1357 4.1222 4.1222 4.1217 4.1192 4.1178 4.1139 4.1135 4.1125 4.1035 4.1025 4.1023 4.0971 4.0969 4.0915 4.0915 4.0914 4.0836 4.0804 4.0803 4.0722 4.065 4.065 4.0649 4.0644 4.0637 4.0616 4.0616 4.061 4.0572 4.0563 4.056 4.0545 4.0545 4.0522 4.0519 4.0514 4.0484 4.0467 4.0463 4.0422 4.0392 4.0388 4.0385 4.0385 4.0383 4.038 4.0379 4.0375 4.0364 4.0353 4.0344];
%# get coordinates of all the points
nPoints = length(curve);
allCoord = [1:nPoints;curve]'; %'# SO formatting
%# pull out first point
firstPoint = allCoord(1,:);
%# get vector between first and last point - this is the line
lineVec = allCoord(end,:) - firstPoint;
%# normalize the line vector
lineVecN = lineVec / sqrt(sum(lineVec.^2));
%# find the distance from each point to the line:
%# vector between all points and first point
vecFromFirst = bsxfun(@minus, allCoord, firstPoint);
%# To calculate the distance to the line, we split vecFromFirst into two
%# components, one that is parallel to the line and one that is perpendicular
%# Then, we take the norm of the part that is perpendicular to the line and
%# get the distance.
%# We find the vector parallel to the line by projecting vecFromFirst onto
%# the line. The perpendicular vector is vecFromFirst - vecFromFirstParallel
%# We project vecFromFirst by taking the scalar product of the vector with
%# the unit vector that points in the direction of the line (this gives us
%# the length of the projection of vecFromFirst onto the line). If we
%# multiply the scalar product by the unit vector, we have vecFromFirstParallel
scalarProduct = dot(vecFromFirst, repmat(lineVecN,nPoints,1), 2);
vecFromFirstParallel = scalarProduct * lineVecN;
vecToLine = vecFromFirst - vecFromFirstParallel;
%# distance to line is the norm of vecToLine
distToLine = sqrt(sum(vecToLine.^2,2));
%# plot the distance to the line
figure('Name','distance from curve to line'), plot(distToLine)
%# now all you need is to find the maximum
[maxDist,idxOfBestPoint] = max(distToLine);
%# plot
figure, plot(curve)
hold on
plot(allCoord(idxOfBestPoint,1), allCoord(idxOfBestPoint,2), 'or')
-
0Спасибо, мне очень нравится это решение! Я должен признать, что мне трудно следить за тем, как вы вычислили расстояние от линии до точки?
-
0Я согласен, что это не было хорошо прокомментированной строкой. Я попытался описать это немного лучше. Кто бы мог подумать, что геометрия в конечном итоге пригодится?
В случае, если кому-то нужна рабочая версия кода Matlab Python, размещенная Jonas выше.
import numpy as np
curve = [8.4663, 8.3457, 5.4507, 5.3275, 4.8305, 4.7895, 4.6889, 4.6833, 4.6819, 4.6542, 4.6501, 4.6287, 4.6162, 4.585, 4.5535, 4.5134, 4.474, 4.4089, 4.3797, 4.3494, 4.3268, 4.3218, 4.3206, 4.3206, 4.3203, 4.2975, 4.2864, 4.2821, 4.2544, 4.2288, 4.2281, 4.2265, 4.2226, 4.2206, 4.2146, 4.2144, 4.2114, 4.1923, 4.19, 4.1894, 4.1785, 4.178, 4.1694, 4.1694, 4.1694, 4.1556, 4.1498, 4.1498, 4.1357, 4.1222, 4.1222, 4.1217, 4.1192, 4.1178, 4.1139, 4.1135, 4.1125, 4.1035, 4.1025, 4.1023, 4.0971, 4.0969, 4.0915, 4.0915, 4.0914, 4.0836, 4.0804, 4.0803, 4.0722, 4.065, 4.065, 4.0649, 4.0644, 4.0637, 4.0616, 4.0616, 4.061, 4.0572, 4.0563, 4.056, 4.0545, 4.0545, 4.0522, 4.0519, 4.0514, 4.0484, 4.0467, 4.0463, 4.0422, 4.0392, 4.0388, 4.0385, 4.0385, 4.0383, 4.038, 4.0379, 4.0375, 4.0364, 4.0353, 4.0344]
nPoints = len(curve)
allCoord = np.vstack((range(nPoints), curve)).T
np.array([range(nPoints), curve])
firstPoint = allCoord[0]
lineVec = allCoord[-1] - allCoord[0]
lineVecNorm = lineVec / np.sqrt(np.sum(lineVec**2))
vecFromFirst = allCoord - firstPoint
scalarProduct = np.sum(vecFromFirst * np.matlib.repmat(lineVecNorm, nPoints, 1), axis=1)
vecFromFirstParallel = np.outer(scalarProduct, lineVecNorm)
vecToLine = vecFromFirst - vecFromFirstParallel
distToLine = np.sqrt(np.sum(vecToLine ** 2, axis=1))
idxOfBestPoint = np.argmax(distToLine)
Выбор модели теоретической модели точки состоит в том, что она уже учитывает количество параметров. Поэтому вам не нужно искать локоть, вам нужно найти минимум.
Поиск локтя кривой применим только при использовании подгонки. Даже тогда метод, который вы выбираете для выбора локтя, в определенном смысле устанавливает штраф за количество параметров. Чтобы выбрать локоть, вы хотите минимизировать расстояние от начала координат до кривой. Относительное взвешивание двух измерений при расчете расстояния создаст присущий ему штрафный срок. Критерий информационной теоремы задает эту метрику на основе количества параметров и количества выборок данных, используемых для оценки модели.
Рекомендация в нижней строке: используйте BIC и возьмите минимум.
-
2Но нахождение финитума неоптимально. Т.е., если вы посмотрите на кривую BIC, для элемента в позиции 100 будет вычислен минимум. Но разница между сложностью 20 и 100 довольно мала - слишком большой выигрыш в дальнейшей цветовой модели.
-
4Итак, вы говорите, что BIC имеет недостаточный штраф за сложность модели (что может быть правдой, хотя, по моему мнению, это не так). Мой аргумент заключается в том, что выбор колена кривой с помощью какого-либо метода создает специальный неизвестный штрафной член. Если вам не нравится ответ, предоставленный BIC или AIC или любым другим методом, основанным на IC, вам лучше было бы разработать штрафной термин и использовать его. Просто мое мнение.
Во-первых, быстрый обзор исчислений: первая производная f' каждого графика представляет собой скорость, с которой графическая диаграмма функции f меняется. Вторая производная f'' представляет собой скорость, с которой изменяется f'. Если f'' мал, это означает, что график меняет направление в скромном темпе. Но если f'' велико, это означает, что график быстро меняет направление.
Вы хотите выделить точки, в которых f'' является наибольшим по области графика. Это будут кандидаты для выбора оптимальной модели. Какой пункт вы выбираете, вам придется решать, так как вы точно не указали, насколько вы цените фитнес и сложность.
-
0Идея определенно верна, но первоначальная проблема остается; как вы определяете это пороговое значение, после которого вы решаете, что скорость изменения слишком мала или слишком высока. Как я уже говорил, у меня есть большое количество экспериментов, из-за которых трудно установить общее значение для всех случаев.
-
0Как правило, вы можете просто выбрать наибольшее
f''.
Таким образом, одним из способов решения этой проблемы было бы две поводки двух линий к локусу L. Но поскольку на одной части кривой есть только несколько точек (как я упоминал в комментарии), финишная линия принимает удар, если вы не обнаружите, какие точки разнесены и интерполируются между ними, чтобы создать более однородную серию и затем используйте RANSAC, чтобы найти две строки, подходящие для L - немного запутанные, но не невозможные.
Итак, здесь более простое решение - графики, которые вы указали, выглядят так, как они делают, благодаря масштабированию MATLAB (очевидно). Таким образом, все, что я сделал, сводило к минимуму расстояние от "источника" до ваших точек, используя информацию о масштабах.
Обратите внимание: Оценка происхождения может быть значительно улучшена, но я оставлю это вам.
Здесь код:
%% Order
curve = [8.4663 8.3457 5.4507 5.3275 4.8305 4.7895 4.6889 4.6833 4.6819 4.6542 4.6501 4.6287 4.6162 4.585 4.5535 4.5134 4.474 4.4089 4.3797 4.3494 4.3268 4.3218 4.3206 4.3206 4.3203 4.2975 4.2864 4.2821 4.2544 4.2288 4.2281 4.2265 4.2226 4.2206 4.2146 4.2144 4.2114 4.1923 4.19 4.1894 4.1785 4.178 4.1694 4.1694 4.1694 4.1556 4.1498 4.1498 4.1357 4.1222 4.1222 4.1217 4.1192 4.1178 4.1139 4.1135 4.1125 4.1035 4.1025 4.1023 4.0971 4.0969 4.0915 4.0915 4.0914 4.0836 4.0804 4.0803 4.0722 4.065 4.065 4.0649 4.0644 4.0637 4.0616 4.0616 4.061 4.0572 4.0563 4.056 4.0545 4.0545 4.0522 4.0519 4.0514 4.0484 4.0467 4.0463 4.0422 4.0392 4.0388 4.0385 4.0385 4.0383 4.038 4.0379 4.0375 4.0364 4.0353 4.0344];
x_axis = 1:numel(curve);
points = [x_axis ; curve ]'; %' - SO formatting
%% Get the scaling info
f = figure(1);
plot(points(:,1),points(:,2));
ticks = get(get(f,'CurrentAxes'),'YTickLabel');
ticks = str2num(ticks);
aspect = get(get(f,'CurrentAxes'),'DataAspectRatio');
aspect = [aspect(2) aspect(1)];
close(f);
%% Get the "origin"
O = [x_axis(1) ticks(1)];
%% Scale the data - now the scaled values look like MATLAB' idea of
% what a good plot should look like
scaled_O = O.*aspect;
scaled_points = bsxfun(@times,points,aspect);
%% Find the closest point
del = sum((bsxfun(@minus,scaled_points,scaled_O).^2),2);
[val ind] = min(del);
best_ROC = [ind curve(ind)];
%% Display
plot(x_axis,curve,'.-');
hold on;
plot(O(1),O(2),'r*');
plot(best_ROC(1),best_ROC(2),'k*');
Результаты:
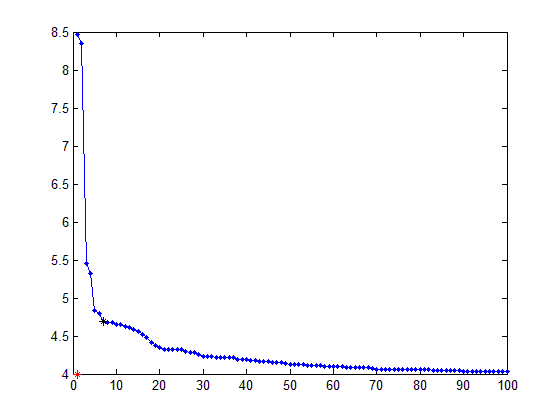
ТАКЖЕ для кривой Fit(maximize) вам нужно будет перейти в начало до [x_axis(1) ticks(end)].
-
0интересная идея, моя единственная проблема заключается в том, что вам нужно составить график и использовать автоматическое масштабирование MATLAB, чтобы найти источник. Это не будет хорошо масштабироваться, особенно если учесть, что у меня есть более миллиона таких кривых для обработки на лету. Xaxis всегда гарантированно начинается с 1, но я не ограничен по оси Yaxis ... и, чтобы ответить на ваш вопрос, форма почти произвольна, хотя я ожидаю быстрого взлета / падения в начале кривой
-
0Так что, я полагаю, проблема в том, чтобы выяснить, какое автоматическое масштабирование MATLAB ... проверит.
Вот решение, данное Джонасом, реализованное в R:
elbow_finder <- function(x_values, y_values) {
# Max values to create line
max_x_x <- max(x_values)
max_x_y <- y_values[which.max(x_values)]
max_y_y <- max(y_values)
max_y_x <- x_values[which.max(y_values)]
max_df <- data.frame(x = c(max_y_x, max_x_x), y = c(max_y_y, max_x_y))
# Creating straight line between the max values
fit <- lm(max_df$y ~ max_df$x)
# Distance from point to line
distances <- c()
for(i in 1:length(x_values)) {
distances <- c(distances, abs(coef(fit)[2]*x_values[i] - y_values[i] + coef(fit)[1]) / sqrt(coef(fit)[2]^2 + 1^2))
}
# Max distance point
x_max_dist <- x_values[which.max(distances)]
y_max_dist <- y_values[which.max(distances)]
return(c(x_max_dist, y_max_dist))
}
Простым и интуитивным способом можно сказать, что
Если мы рисуем две линии из любой точки кривой в обе конечные точки кривой, то точка, в которой эти две линии составляют наименьший угол в градусах, является искомой точкой.
Здесь две линии могут быть визуализированы как руки и точка как точка локтя!
Двойной производный метод. Однако он не работает хорошо для шумных данных. Для вывода вы просто найдете максимальное значение d2 для идентификации локтя. Эта реализация выполняется в R.
elbow_finder <- function(x_values, y_values) {
i_max <- length(x_values) - 1
# First and second derived
first_derived <- list()
second_derived <- list()
# First derived
for(i in 2:i_max){
slope1 <- (y_values[i+1] - y_values[i]) / (x_values[i+1] - x_values[i])
slope2 <- (y_values[i] - y_values[i-1]) / (x_values[i] - x_values[i-1])
slope_avg <- (slope1 + slope2) / 2
first_derived[[i]] <- slope_avg
}
first_derived[[1]] <- NA
first_derived[[i_max+1]] <- NA
first_derived <- unlist(first_derived)
# Second derived
for(i in 3:i_max-1){
d1 <- (first_derived[i+1] - first_derived[i]) / (x_values[i+1] - x_values[i])
d2 <- (first_derived[i] - first_derived[i-1]) / (x_values[i] - x_values[i-1])
d_avg <- (d1 + d2) / 2
second_derived[[i]] <- d_avg
}
second_derived[[1]] <- NA
second_derived[[2]] <- NA
second_derived[[i_max]] <- NA
second_derived[[i_max+1]] <- NA
second_derived <- unlist(second_derived)
return(list(d1 = first_derived, d2 = second_derived))
}
Если хотите, я перевел его на R как упражнение для себя (простите за мой неоптимизированный стиль кодирования). * Применял его, чтобы найти оптимальное количество кластеров на k-средних - работал довольно хорошо.
elbow.point = function(x){
elbow.curve = c(x)
nPoints = length(elbow.curve);
allCoord = cbind(c(1:nPoints),c(elbow.curve))
# pull out first point
firstPoint = allCoord[1,]
# get vector between first and last point - this is the line
lineVec = allCoord[nPoints,] - firstPoint;
# normalize the line vector
lineVecN = lineVec / sqrt(sum(lineVec^2));
# find the distance from each point to the line:
# vector between all points and first point
vecFromFirst = lapply(c(1:nPoints), function(x){
allCoord[x,] - firstPoint
})
vecFromFirst = do.call(rbind, vecFromFirst)
rep.row<-function(x,n){
matrix(rep(x,each=n),nrow=n)
}
scalarProduct = matrix(nrow = nPoints, ncol = 2)
scalarProduct[,1] = vecFromFirst[,1] * rep.row(lineVecN,nPoints)[,1]
scalarProduct[,2] = vecFromFirst[,2] * rep.row(lineVecN,nPoints)[,2]
scalarProduct = as.matrix(rowSums(scalarProduct))
vecFromFirstParallel = matrix(nrow = nPoints, ncol = 2)
vecFromFirstParallel[,1] = scalarProduct * lineVecN[1]
vecFromFirstParallel[,2] = scalarProduct * lineVecN[2]
vecToLine = lapply(c(1:nPoints), function(x){
vecFromFirst[x,] - vecFromFirstParallel[x,]
})
vecToLine = do.call(rbind, vecToLine)
# distance to line is the norm of vecToLine
distToLine = as.matrix(sqrt(rowSums(vecToLine^2)))
##
which.max(distToLine)
}
вход x функции должен быть списком/вектором с вашими значениями
Я некоторое время работаю над обнаружением точки колена/локтя. Я вовсе не эксперт. Некоторые методы, которые могут иметь отношение к этой проблеме.
DFDT обозначает динамический порог первой деривации. Он вычисляет первую производную и использует алгоритм Thresholding для определения точки колена/локтя. DSDT похож, но использует вторую производную, моя оценка показывает, что они имеют схожие характеристики.
S-метод является расширением L-метода. L-метод подходит для двух прямых линий к вашей кривой, перехват между двумя линиями - точка колена/локтя. Лучшая подгонка найдена путем обхода общих точек, установки линий и оценки MSE (средняя квадратическая ошибка). S-метод соответствует 3 прямым линиям, что повышает точность, но требует еще нескольких вычислений.
Весь мой код является общедоступным в GitHub. Кроме того, эта статья поможет вам найти дополнительную информацию по этой теме. Это всего лишь четыре страницы, поэтому их легко читать. Вы можете использовать код, и если вы хотите обсудить любой из этих методов, не стесняйтесь это делать.
Ещё вопросы
- 1SSL не работает на Android 2.2 (только в 2.3)
- 0Как воссоздать объект JSON
- 0ng Cordova file_uri к base64
- 1Является ли Material TextAppearance полезным для обработки различных textSize
- 0Найдите поле ввода с определенным идентификатором и атрибутом обновления, используя jQuery
- 1Скребок продолжает сканировать идентичные ссылки
- 0Написать Html Img ID с помощью JavaScript
- 1Как объединить серию на основе индекса даты, чтобы сформировать df без потери данных
- 1Ошибка Java JNI DPAPI java.lang.UnsatisfiedLinkError:
- 0Как сделать перенаправление в новой вкладке с «POST» с помощью jquery?
- 0координаты XYZ из reprojectImageTo3D opencv
- 1Бесконечный цикл с обновленным атрибутом внутри события изменения базовой модели
- 1Показ промежуточной рекламы adMob, когда пользователь выходит из приложения, но не намеренно
- 1Атрибут Web.config xmlns при чтении его в xslt.Problems
- 0Spring Data: findByEntityNot () во многих отношениях
- 1Новый экземпляр программы создается при прикосновении к тегу NFC
- 1Счетчик значений по группе не показывает счетчик значений NULL / NA в пандах
- 1GSON преобразует ранее сохраненный список в ArrayList LinkedTreeMaps при получении из общих префов
- 0Передача вектора в функцию
- 1Булевский DataFrame из серии с самим собой в Pandas
- 1Scrapy - Получение 504 тайм-аута шлюза после первых запросов
- 1pandas.date_range, приводящий к повторяющемуся «липкому» предупреждению: «414: FutureWarning:« сводка »устарела и будет удалена в будущей версии».
- 0Стек Mean.js - экспорт.читайте с помощью функций findOne и find, вызывайте в Angularjs
- 1Xamarin Profiler вылетает приложение с самого начала
- 1notify () против notifyAll ()?
- 1Xming: почему JFrame потерял фокус, когда установлен Undecorated (true)?
- 0угловой JS $ HTTP вернуть true или false
- 1Скрыть StatusBar в Trusted Web Activity
- 1Как заменить вхождения с Javascript внутри разделителей?
- 0Как я могу загрузить файлы CoffeeScript из пакетов Bower с помощью веб-пакета?
- 1Java-сервлеты: проверка XML на xsd
- 0Стрлен переменной GET
- 0PHP Curl Check 404: всегда возвращать HTTPCODE 200 OK
- 0Вычеркнуть несколько текстов в опции выбора
- 1Список радиокнопок
- 1Проверка кода JavaScript на наличие опечаток в Notepad ++
- 1Цикл while для определения, является ли введенное значение двойным
- 1Подключение USB-устройств к эмулятору Android
- 0Ошибка JavaScript при попытке $ .get
- 0Как использовать app / Resources / public в Symfony2
- 0Сосредоточиться на выбранной дате после отправки формы в функции onSelect
- 0как заменить конкретный символ из строки в JQuery
- 0Symfony 2 PHP Template Engine рендеринг объектов
- 1Применить цвет к определенному слову в строке
- 1Интерполяция в пандах по горизонтали не зависит от каждой строки
- 1Сбой смешивания с ObservableAsPropertyHelper
- 1У классификатора нет сопутствующего объекта, и, следовательно, он должен быть инициализирован здесь
- 1Открытие электронного письма с несколькими вложениями, в то время как выбор ограничен ТОЛЬКО почтовыми приложениями?
- 0Заставить AngularJS ui-router / app ждать данные $ http для предотвращения FOUC
- 1Категориальные переменные в несколько столбцов
