Алгоритм дерева суффиксов Укконена на простом английском
Я чувствую себя немного толстым в этот момент. Я потратил дни, пытаясь полностью обернуть голову вокруг конструкции дерева суффиксов, но поскольку у меня нет математического фона, многие из объяснений ускользают от меня, когда они начинают чрезмерно использовать математическую символику. Самое близкое к хорошему объяснению, которое я нашел, Быстрый поиск строк с деревьями суффикса, но он замалчивает различные точки и некоторые аспекты алгоритма остаются неясными.
Пошаговое объяснение этого алгоритма здесь на Qaru было бы неоценимым для многих других, кроме меня, я уверен.
Для справки, здесь статья Укконена по алгоритму: http://www.cs.helsinki.fi/u/ukkonen/SuffixT1withFigs.pdf
Мое основное понимание, до сих пор:
- Мне нужно перебирать каждый префикс P заданной строки T
- Мне нужно перебирать каждый суффикс S в префиксе P и добавлять его к дереву
- Чтобы добавить суффикс S к дереву, мне нужно выполнить итерацию по каждому символу в S, причем итерации состоят либо в том, что они идут по существующей ветке, которая начинается с того же набора символов C в S и может разделить ребро на потомство узлы, когда я получаю различный символ в суффиксе, ИЛИ, если не было подходящего края, чтобы спуститься. Если для C не найдено совпадающего края, для C создается новый край листа.
Основным алгоритмом является O (n 2), как указано в большинстве объяснений, так как нам нужно пройти все префиксы, тогда нам нужно пройти через каждый из суффиксы для каждого префикса. Алгоритм Укконена, по-видимому, уникален из-за метода указателя суффиксов, который он использует, хотя я думаю, что это то, что у меня возникли проблемы с пониманием.
У меня также возникли проблемы с пониманием:
- точно, когда и как "активная точка" назначается, используется и изменяется
- то, что происходит с аспектом канонизации алгоритма
- Почему реализации, которые я видел, должны "фиксировать" ограничивающие переменные, которые они используют
Вот завершенный С# исходный код. Он работает не только корректно, но и поддерживает автоматическую канонизацию и отображает более удобный текстовый график вывода. Исходный код и выходные данные:
Обновление 2017-11-04
Спустя много лет я нашел новое использование для деревьев суффиксов и реализовал алгоритм в JavaScript. Гист внизу. Он должен быть без ошибок. Выгрузите его в файл js, npm install chalk из того же места, а затем запустите с помощью node.js, чтобы увидеть какой-нибудь яркий выход. Там урезанная версия в том же Gist, без какого-либо кода отладки.
https://gist.github.com/axefrog/c347bf0f5e0723cbd09b1aaed6ec6fc6
-
0У меня было довольно много проблем, чтобы реализовать эту структуру данных самостоятельно. В конце концов я нашел эту статью и сумел ее реализовать. Большим плюсом является то, что у вас есть пошаговый пример для довольно длинной строки, чтобы вы могли увидеть, что вам следует делать. Пожалуйста, ознакомьтесь с этой статьей, и я буду очень рад дать советы, где это необходимо. Я не решаюсь дать еще одно полномасштабное объяснение, поскольку в Интернете уже есть немало таких людей.Ivaylo Strandjev
-
2Вы смотрели на описание, данное в книге Дэна Гусфилда ? Я нашел это полезным.jogojapan
6 ответов
Ниже приведена попытка описать алгоритм Укконена, сначала продемонстрировав, что он делает, когда строка проста (т.е. не содержит повторяющихся символов), а затем расширяет ее до полного алгоритма.
Во-первых, несколько предварительных утверждений.
-
То, что мы строим, в основном похоже на поисковое трю. Так что является корнем node, края, выходящие из него, приводящие к новым узлам, и другие ребра, выходящие из них, и т.д.
-
Но. В отличие от поискового тэра метки границ не одиноки персонажи. Вместо этого каждое ребро помечено с помощью пары целых чисел
[from,to]. Это указатели на текст. В этом смысле каждый edge несет строчную метку произвольной длины, но принимает только O (1) пространство (два указателя).
Основной принцип
Я хотел бы сначала продемонстрировать, как создать дерево суффиксов особенно простая строка, строка без повторных символов:
abc
Алгоритм работает пошагово, слева направо. Для каждого символа строки существует один шаг. Каждый шаг может включать в себя более одной отдельной операции, но мы увидим (см. Окончательные замечания в конце), что общее число операций равно O (n).
Итак, мы начинаем слева и сначала вставляем только один символ
a, создав ребро из корня node (слева) на лист,
и обозначая его как [0,#], что означает, что край представляет собой
подстрока, начинающаяся в позиции 0 и заканчивающаяся на текущем конце. я
используйте символ # для обозначения текущего конца, который находится в позиции 1
(сразу после a).
Итак, у нас есть начальное дерево, которое выглядит так:
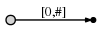
И что это значит:
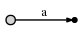
Теперь мы переходим к позиции 2 (сразу после b). Наша цель на каждом шаге
заключается в том, чтобы вставить все суффиксы до текущей позиции. Мы делаем это
по
- расширение существующего
a-edge доab - вставка одного нового края для
b
В нашем представлении это выглядит как
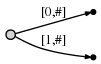
И что это значит:
Мы наблюдаем две вещи:
- Представление edge для
ab- это тот же, что и раньше в исходном дереве:[0,#]. Его значение автоматически изменилось потому что мы обновили текущую позицию#от 1 до 2. - Каждый ребро потребляет пространство O (1), поскольку он состоит только из двух указатели в текст, независимо от того, сколько символов оно представляет.
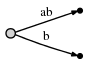
Затем мы снова увеличиваем позицию и обновляем дерево, добавляя
a c для каждого существующего края и вставки одного нового ребра для нового
суффикс c.
В нашем представлении это выглядит как
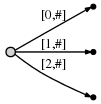
И что это значит:
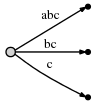
Мы наблюдаем:
- Дерево - это правильное дерево суффикса до текущей позиции после каждого шага
- Существует столько шагов, сколько символов в тексте
- Объем работы на каждом этапе равен O (1), поскольку все существующие ребра
автоматически обновляются, увеличивая
#и вставляя одно новое ребро для конечного символа может быть выполнено в O (1) время. Следовательно, для строки длины n требуется только время O (n).
Первое расширение: Простые повторения
Конечно, это работает так хорошо только потому, что наша строка не содержат любые повторения. Теперь посмотрим на более реалистичную строку:
abcabxabcd
Он начинается с abc, как в предыдущем примере, затем повторяется ab
и затем x, а затем abc повторяется, а затем d.
Шаги с 1 по 3:. После первых трех шагов мы имеем дерево из предыдущего примера:
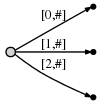
Шаг 4: Мы перемещаем # в позицию 4. Это неявно обновляет все существующие
края к этому:
и нам нужно вставить последний суффикс текущего шага, a, at
корень.
Прежде чем мы это сделаем, введем еще две переменные (в дополнение к
#), которые, конечно, были там все время, но мы не использовали
их до сих пор:
- Активная точка , которая является тройной
(active_node,active_edge,active_length) -
remainder, который является целым числом, указывающим, сколько новых суффиксов нам нужно вставить
Точный смысл этих двух скоро станет ясным, но пока позвольте сказать:
- В простом примере
abcактивная точка всегда была(root,'\0x',0), т.е.active_nodeбыл корнем node,active_edgeбыл указан как нулевой символ'\0x', аactive_lengthбыл равен нулю. Эффект от этого заключался в том, что один новый край, который мы вставили на каждый шаг, вставили в корень node как только что созданный край. Мы скоро увидим, почему тройка необходима для представляют эту информацию. -
remainderвсегда был установлен в 1 в начале каждого шаг. Смысл этого заключался в том, что количество суффиксов, которые мы имели активно вставлять в конце каждого шага 1 (всегда просто конечный символ).
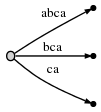
Теперь это изменится. Когда мы вставляем текущий финальный
символ a в корне, мы замечаем, что уже существует исходящий
край, начинающийся с a, в частности: abca. Вот что мы делаем в
такой случай:
- не не вставляем свежий край
[4,#]в корневой каталог node. Вместо этого мы просто заметим, что суффиксaуже находится в нашем дерево. Он заканчивается в середине более длинного края, но мы не обеспокоенный этим. Мы просто оставляем вещи такими, какие они есть. - Мы установите для активной точки значение
(root,'a',1). Это означает, что точка теперь находится где-то посередине выходящего края корня node, который начинается сa, в частности, после позиции 1 на этом ребре. Мы обратите внимание, что край задается просто его первым символa. Этого достаточно, потому что может быть только одно ребро начиная с любого конкретного символа (подтвердите, что это верно после прочтения всего описания). - Мы также увеличиваем
remainder, поэтому в начале следующего шага это будет 2.
Наблюдение:. Когда окончательный суффикс , который нам нужно вставить,
существуют в дереве уже, само дерево не изменено вообще (мы обновляем только активную точку и remainder). Дерево
не является точным представлением дерева суффиксов до
текущая позиция больше, но она содержит все суффиксы (потому что окончательный
суффикс a содержится неявно). Следовательно, помимо обновления
переменные (которые имеют фиксированную длину, поэтому это O (1)),
без работы на этом шаге.
Шаг 5: Мы обновляем текущую позицию # до 5. Это
автоматически обновляет дерево до этого:
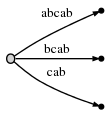
И , потому что remainder равен 2, нам нужно вставить два финальных
суффиксы текущего положения: ab и b. Это в основном потому, что:
- Суффикс
aс предыдущего шага никогда не был должным образом вставлено. Так оно и осталось, и поскольку мы продвинулись теперь он вырос отaдоab. - И нам нужно вставить новый конечный ребро
b.
На практике это означает, что мы переходим к активной точке (что указывает на
за a на том, что теперь является краем abcab), и вставьте
текущий конечный символ b. Но: Опять же, оказывается, что b есть
также уже присутствующие на том же ребре.
Итак, опять же, мы не меняем дерево. Мы просто:
- Обновить активную точку до
(root,'a',2)(тот же node и край как и раньше, но теперь мы указываем наb) - Увеличьте
remainderдо 3, потому что мы все еще не имеем должным образом вставил последний край из предыдущего шага, и мы не вставляем текущий конечный край.
Чтобы быть ясным: нам нужно было вставить ab и b на текущем шаге, но
потому что ab уже был найден, мы обновили активную точку и сделали
даже не пытайтесь вставить b. Зачем? Потому что если ab находится в дереве,
каждый суффикс (включая b) должен находиться в дереве,
слишком. Возможно, только неявно, но он должен быть там, из-за
мы до сих пор строили дерево.
Мы переходим к шагу 6, увеличивая #. Дерево
автоматически обновляется до:
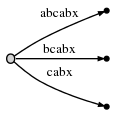
Поскольку remainder - 3, мы должны вставить abx, bx и
x. Активная точка сообщает нам, где ab заканчивается, поэтому нам нужно только
прыгайте туда и вставьте x. Действительно, x еще нет, поэтому мы
разделите край abcabx и вставьте внутренний node:
Представления ребер по-прежнему являются указателями на текст, поэтому расщепление и вставка внутреннего node можно выполнить в течение O (1).
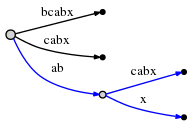
Итак, мы имеем дело с abx и декрементом remainder до 2. Теперь мы
необходимо вставить следующий оставшийся суффикс, bx. Но прежде чем мы это сделаем
нам нужно обновить активную точку. Правило для этого, после расщепления
и вставка края, будет называться Правило 1 ниже, и оно применяется всякий раз, когда
active_node является корнем (мы будем изучать правило 3 для других случаев далее
ниже). Вот правило 1:
После вставки из корня
active_nodeостается rootactive_edgeустанавливается на первый символ нового суффикса we необходимо вставить, т.е.bactive_lengthуменьшается на 1
Следовательно, новая тройка с активной точкой (root,'b',1) указывает, что
следующая вставка должна быть сделана на краю bcabx, за 1 символом,
то есть за b. Мы можем определить точку ввода в O (1) время и
проверьте, присутствует ли x или нет. Если бы он присутствовал, мы
закончит текущий шаг и оставит все так, как есть. Но x
нет, поэтому мы вставляем его, разбивая ребро:
<Т411 >
Опять же, это заняло время O (1), и мы обновили remainder до 1 и
активная точка до (root,'x',0), как указано в правиле 1.
Но есть еще одна вещь, которую нам нужно сделать. Мы будем называть это Правило 2:
Если мы разделим ребро и вставим новый node, и если это не первый node, созданный во время текущего шага, мы соединяем ранее вставил node и новый node через специальный указатель, суффикс ссылка. Позже мы увидим, почему это полезно. Вот что мы получаем, суффикс-ссылка представляется в виде точечного ребра:
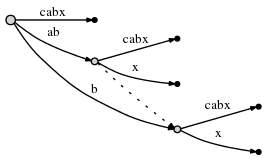
Нам еще нужно вставить окончательный суффикс текущего шага,
x. Поскольку компонент active_length активного node упал
до 0, окончательная вставка выполняется непосредственно в корне. Поскольку нет
исходящий край в корне node, начиная с x, мы вставляем новый
Край:
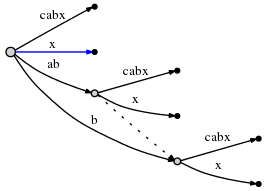
Как мы видим, на текущем этапе были сделаны все остальные вставки.
Переходим к шагу 7, установив #= 7, который автоматически добавляет следующий символ,
a, ко всем ребрам листа, как всегда. Затем мы пытаемся вставить новый финал
символ в активную точку (корень), и найдите, что она есть
уже. Поэтому мы завершаем текущий шаг, не вставляя ничего и
обновите активную точку до (root,'a',1).
В шаге 8, #= 8 добавим b, и, как видно ранее, это только
означает, что мы обновляем активную точку до (root,'a',2) и увеличиваем remainder, не делая
ничего другого, потому что b уже присутствует. Однако мы замечаем (в O (1) время), что активная точка
теперь находится в конце края. Мы размышляем об этом, переставляя его на
(node1,'\0x',0). Здесь я использую node1 для обозначения
внутренний node край ab заканчивается на.
Затем, в шаге #= 9, нам нужно вставить 'c', и это поможет нам
понять окончательный трюк:
Второе расширение: использование суффиксных ссылок
Как всегда, обновление # автоматически добавляет c к краям листа
и мы переходим к активной точке, чтобы увидеть, можем ли мы вставить 'c'. Он поворачивается
out 'c' существует уже на этом ребре, поэтому мы устанавливаем активную точку в
(node1,'c',1), increment remainder и ничего не делать.
Теперь в шаге #= 10, remainder is 4, и поэтому нам сначала нужно вставить
abcd (который остается от 3 шагов назад), вставив d в активную
точка.
Попытка вставить d в активную точку вызывает разбиение края
O (1):
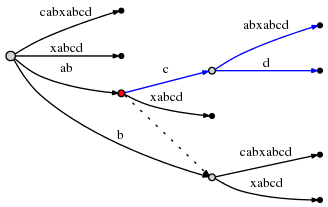
active_node, из которого был инициирован раскол, отмечен в
красный выше. Вот окончательное правило, Правило 3:
После разделения ребра на
active_node, который не является корнем node, мы следуем ссылке суффикса, выходящей из этого node, если есть любой, и resetactive_nodeк node, на который указывает. Если там есть без суффикса, мы устанавливаемactive_nodeв корневой каталог.active_edgeиactive_lengthостаются неизменными.
Итак, активная точка теперь (node2,'c',1), а node2 отмечена в
красный ниже:
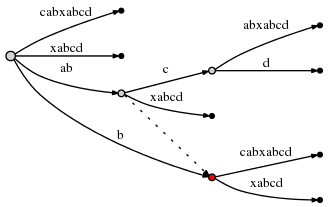
Так как вставка abcd завершена, мы уменьшаем remainder до
3 и рассмотрим следующий оставшийся суффикс текущего шага,
bcd. Правило 3 устанавливает активную точку только вправо node, а край
поэтому вставка bcd может быть выполнена путем простого вставки ее окончательного символа
d в активной точке.
Выполнение этого приводит к другому разделению краев и из-за правила 2, мы должен создать ссылку суффикса из ранее вставленной node в новую один:
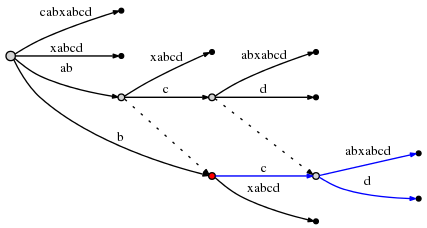
Мы наблюдаем: Суффикс-ссылки позволяют нам reset активную точку, поэтому мы может сделать следующую оставшуюся вставку при усилении O (1). Посмотрите на выше, чтобы подтвердить, что действительно node на ярлыке ab связано с node at b (его суффикс), а node at abc связан с bc.
Текущий шаг еще не завершен. remainder теперь 2, и мы
необходимо снова следовать правилу 3 до reset активной точки. Поскольку
текущий active_node (красный выше) не имеет суффикса, мы reset до
корень. Активная точка теперь (root,'c',1).
Следовательно, следующая вставка возникает на одном исходящем краю корня node
чей ярлык начинается с c: cabxabcd, за первым символом,
т.е. за c. Это вызывает другое разделение:
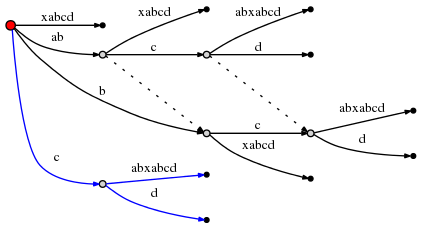
И поскольку это связано с созданием нового внутреннего node, мы следуем правило 2 и установить новую суффиксную ссылку из ранее созданного внутреннего node:
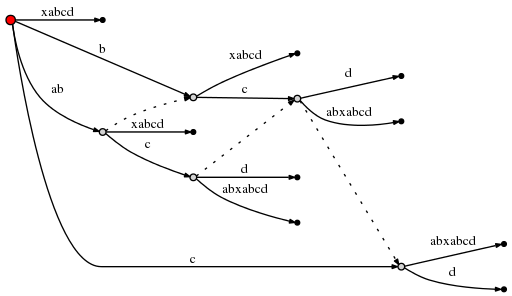
(Я использую Graphviz Dot для этих маленьких графики. Новая ссылка на суффикс заставила точку переустановить существующие края, поэтому тщательно проверьте, чтобы убедиться, что единственное, что было вставленный выше, представляет собой новую ссылку суффикса.)
При этом remainder может быть установлен в 1, а так как active_node
root, мы используем правило 1 для обновления активной точки до (root,'d',0). Эта
означает, что окончательная вставка текущего шага состоит в том, чтобы вставить один d
у корня:
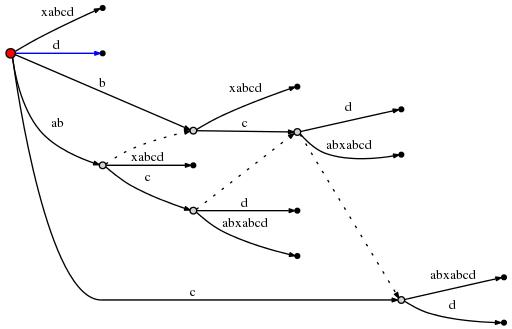
Это был последний шаг, и мы закончили. Существует число final наблюдения:
-
На каждом шаге мы перемещаем
#вперед на 1 позицию. Это автоматически обновляет все листовые узлы в O (1) раз. -
Но это не касается а) любых суффиксов, оставшихся от предыдущего шаги и b) с одним окончательным символом текущего шага.
-
remainderсообщает нам, сколько дополнительных вставок нам нужно делать. Эти вставки соответствуют друг другу до конечных суффиксов строка, которая заканчивается в текущей позиции#. Рассмотрим один после другого и сделать вставку. Важно: Каждая вставка сделано в O (1) раз, так как активная точка указывает нам, где именно go, и нам нужно добавить только один символ в активном точка. Зачем? Поскольку другие символы содержатся неявно (иначе активная точка не будет там, где она есть). -
После каждой такой вставки мы уменьшаем
remainderи следуем суффикс, если он есть. Если нет, мы перейдем к корню (правило 3). Если мы уже находятся в корне, мы модифицируем активную точку, используя правило 1. В в любом случае требуется только время O (1). -
Если во время одной из этих вставок мы обнаруживаем, что персонаж, которого мы хотим для вставки уже есть, мы ничего не делаем и заканчиваем текущий шаг, даже если
remainder> 0. Причина в том, что любой вставками, которые остаются, будут суффиксы того, с которым мы просто пытались делать. Следовательно, они все неявны в текущем дереве. Факт чтоremainder> 0 гарантирует, что мы имеем дело с остальными суффиксами позже. -
Что делать, если в конце алгоритма
remainder> 0? Это будет когда конец текста является подстрокой, которая произошла где-то раньше. В этом случае мы должны добавить один дополнительный символ в конце строки, которая раньше не встречалась. в литературы, обычно знак доллара$используется в качестве символа для что. Почему это важно? → Если позже мы будем использовать заполненное дерево суффиксов для поиска суффиксов, мы должны принимать совпадения, только если они заканчиваются на листе. В противном случае мы получим много ложных совпадений, потому что в дереве неявно содержится много строк, которые не являются суффиксами основной строки. Принуждениеremainderк 0 в конце - это, по сути, способ обеспечить, чтобы все суффиксы заканчивались на листе node. Тем не менее,, если мы хотим использовать дерево для поиска общих подстрок, а не только суффиксов основной строки, этот последний шаг действительно не требуется, как это предлагается в комментарии к OP ниже. -
Итак, какова сложность всего алгоритма? Если текст равен n символов в длину, очевидно, n шагов (или n + 1, если мы добавим знак доллара). На каждом шаге мы ничего не делаем (кроме обновление переменных), или мы делаем вставки
remainder, каждый из которых принимает O (1) время. Посколькуremainderуказывает, сколько раз мы ничего не сделали в предыдущих шагах, и уменьшается на каждую вставку, которую мы делаем теперь общее число раз мы делаем что-то точно n (или п + 1). Следовательно, общая сложность O (n). -
Однако есть одна маленькая вещь, которую я не объяснил должным образом: Может случиться так, что мы следуем ссылке суффикса, обновим активную point, а затем найдите, что его компонент
active_lengthне хорошо работать с новымactive_node. Например, рассмотрим ситуацию например:
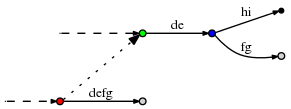
(Пунктирные линии указывают остальную часть дерева. Пунктирная линия представляет собой суффикс.)
Теперь пусть активная точка будет (red,'d',3), поэтому она указывает на место
за f на краю defg. Теперь предположим, что мы сделали необходимые
обновления и теперь следуйте ссылке суффикса, чтобы обновить активную точку
в соответствии с правилом 3. Новая активная точка (green,'d',3). Однако,
d -edge, выходящий из зеленого node, равен de, поэтому он имеет только 2
персонажи. Чтобы найти правильную активную точку, мы, очевидно,
необходимо следовать за этим краем до синего node и reset до (blue,'f',1).
В особенно плохом случае active_length может быть таким же большим, как
remainder, который может быть равен n. И это может произойти
что для нахождения правильной активной точки нам нужно не только перепрыгнуть через один
внутренний node, но, возможно, многие, вплоть до n в худшем случае. Это
означает, что алгоритм имеет скрытую сложность O (n 2), поскольку
на каждом этапе remainder, как правило, O (n), и пост-корректировки
к активному node после того, как ссылка на суффикс может быть O (n) тоже?
Нет. Причина в том, что если мы действительно должны отрегулировать активную точку
(например, от зеленого до синего, как указано выше), что приводит нас к новому node, который
имеет свою собственную суффиксную ссылку, а active_length будет уменьшена. В виде
мы следим за цепочкой суффиксных ссылок, которые мы делаем остальными вставками, active_length может только
уменьшения и количества корректировок активной точки, которые мы можем сделать
способ не может быть больше, чем active_length в любой момент времени. поскольку
active_length никогда не может быть больше remainder и remainder
O (n) не только на каждом шаге, но и на общую сумму приращений
когда-либо сделанное до remainder в течение всего процесса
O (n) тоже количество корректировок активной точки также ограничено
О (п).
-
68Извините, это закончилось немного дольше, чем я надеялся. И я понимаю, что это объясняет ряд тривиальных вещей, которые мы все знаем, в то время как сложные части могут все еще быть не совсем ясными. Давайте отредактируем это в форме вместе.
-
64И я должен добавить, что это не основано на описании, найденном в книге Дэна Гасфилда. Это новая попытка описать алгоритм, сначала рассматривая строку без повторений, а затем обсуждая, как обрабатываются повторения. Я надеялся, что это будет более интуитивно понятно.
Я попытался реализовать Дерево Суффикса с подходом, указанным в jogojapan-ответе, но в некоторых случаях он не работал из-за формулировки, используемой для правил. Более того, я упомянул, что с помощью этого подхода никто не смог реализовать абсолютно правильное дерево суффикса. Ниже я напишу "обзор" jogojapan-ответа с некоторыми изменениями правил. Я также опишу случай, когда мы забудем создавать суффиксные ссылки важные.
Дополнительные используемые переменные
- активная точка - тройной (active_node; active_edge; active_length), показывающий, откуда мы должны начать вставлять новый суффикс.
- остаток - показывает количество суффиксов, которые мы должны добавить явно. Например, если наше слово "abcaabca", а остальное = 3, это означает, что мы должны обработать 3 последних суффикса: bca, ca и a.
Давайте используем концепцию внутреннего node - всех узлов, кроме корня, а листья - внутренних узлов.
Наблюдение 1
Когда окончательный суффикс, который нам нужно вставить, уже существует в дереве, само дерево вообще не изменяется (мы обновляем только active point и remainder).
Наблюдение 2
Если в некоторой точке active_length больше или равно длине текущего края (edge_length), мы перемещаем наш active point вниз, пока edge_length не будет строго больше active_length.
Теперь давайте переопределим правила:
Правило 1
Если после вставки из активного корня node =, активная длина больше 0, то:
- active node не изменен
- активная длина уменьшается
- активная граница сдвигается вправо (к первому символу следующего суффикса, который мы должны вставить)
Правило 2
Если мы создадим новый внутренний node OR, создадим вставку из внутреннего node, и это не первый SUCH внутренний node при текущей шаг, то мы связываем предыдущий SUCH node с ЭТО через суффиксную ссылку.
Это определение Rule 2 отличается от jogojapan ', так как здесь мы учитываем не только вновь созданные внутренние узлы, но и внутренние узлы, из которых мы делаем вставку.
Правило 3
После вставки из активного node, который не является корнем node, мы должны следовать ссылке суффикса и установить активный node на node, на который он указывает. Если нет ссылки на суффикс, установите активный node в корень node. В любом случае активный край и активная длина остаются неизменными.
В этом определении Rule 3 мы также рассмотрим вставки листовых узлов (а не только разделенные узлы).
И, наконец, Observation 3:
Когда символ, который мы хотим добавить в дерево, уже находится на краю, мы, согласно Observation 1, обновляем только active point и remainder, оставляя дерево неизменным. НО, если есть внутренний node, помеченный как необходимая ссылка суффикса, мы должны подключить это node к нашему текущему active node через суффиксную ссылку.
Посмотрим на пример дерева суффиксов для cdddcdc, если мы добавим ссылку суффикса в этом случае, а если нет:
-
Если мы НЕ делаем соединяем узлы через суффиксную ссылку:
- перед добавлением последней буквы c:
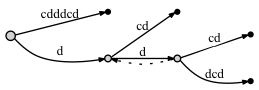
- после добавления последней буквы c:
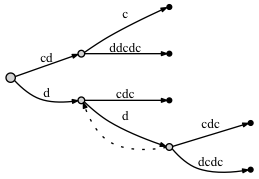
-
Если мы DO соединяем узлы через суффиксную ссылку:
- перед добавлением последней буквы c:
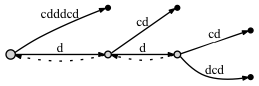
- после добавления последней буквы c:
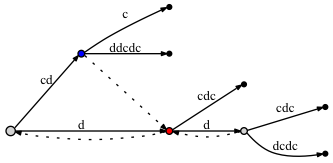
Похоже, нет существенной разницы: во втором случае есть еще две ссылки суффикса. Но эти суффиксные ссылки правильны, и один из них - от синего node до красного - очень важный для нашего подхода с активной точкой. Проблема в том, что если мы не помещаем ссылку на суффикс здесь, позже, когда мы добавим новые буквы в дерево, мы можем опустить добавление некоторых узлов в дерево из-за Rule 3, потому что, согласно ему, если там нет ссылки суффикса, тогда мы должны положить active_node в корень.
Когда мы добавляли последнюю букву к дереву, красный node имел уже существовал, прежде чем мы сделали вставку из синего node (край labled 'c'). Поскольку вставка синего цвета node, мы отмечаем ее как необходимую ссылку суффикса. Затем, опираясь на подход активной точки, active node был установлен на красный node. Но мы не делаем вставку из красного node, так как буква 'c' уже находится на краю. Означает ли это, что синий node должен быть оставлен без ссылки суффикса? Нет, мы должны подключить синий node к красному по ссылке суффикса. Почему это правильно? Поскольку подход активная точка гарантирует, что мы попадаем в нужное место, то есть на следующее место, где мы должны обработать вставку суффикса короче.
Наконец, вот мои реализации дерева суффикса:
Надеюсь, что этот "обзор" в сочетании с подробным ответом jogojapan поможет кому-то реализовать свое собственное Суффикс-дерево.
-
3Большое спасибо и +1 за ваши усилия. Я уверен, что вы правы .. хотя у меня нет времени, чтобы сразу подумать о деталях. Я проверю позже и, возможно, также изменю свой ответ.
-
0Большое спасибо, это действительно помогло. Хотя, не могли бы вы поподробнее рассказать о Наблюдении 3? Например, предоставление диаграмм 2 шагов, которые вводят новую ссылку суффикса. Связан ли узел с активным узлом? (поскольку мы на самом деле не вставляем 2-й узел)
У меня было довольно много проблем для реализации этой структуры данных. В итоге я нашел эту статью и смог ее реализовать. Большим плюсом для этого является то, что у вас есть пошаговый пример для довольно длинной строки, чтобы вы могли видеть, что вам следует делать. Пожалуйста, взгляните на статью, и я буду более счастлив дать советы там, где это необходимо. Я не решаюсь выпустить еще одно полномасштабное объяснение, так как в интернете есть несколько довольно много.
Моя интуиция такова:
После k итераций основного цикла вы создали дерево суффикса, которое содержит все суффиксы полной строки, начинающиеся с первых k символов.
В начале это означает, что дерево суффикса содержит один корень node, который представляет всю строку (это единственный суффикс, начинающийся с 0).
После итераций len (string) у вас есть дерево суффикса, содержащее все суффиксы.
Во время цикла ключ является активной точкой. Я предполагаю, что это представляет собой самую глубокую точку в дереве суффиксов, которая соответствует правильному суффиксу первых k символов строки. (Я считаю, что правильно означает, что суффикс не может быть всей строкой.)
Например, предположим, что вы видели символы abcabc. Активная точка будет представлять точку в дереве, соответствующую суффиксу "abc".
Активная точка представлена (origin, first, last). Это означает, что вы в данный момент находитесь в точке дерева, к которому вы подключились, начиная с начала node и затем подавая символы в строке [first: last]
При добавлении нового символа вы увидите, активна ли активная точка в существующем дереве. Если это так, вы закончите. В противном случае вам нужно добавить новый node в дерево суффиксов в активной точке, вернуться к следующему кратчайшему и снова проверить.
Примечание 1: Указатели суффиксов дают ссылку на следующее кратчайшее соответствие для каждого node.
Примечание 2: Когда вы добавляете новый node и резервную копию, вы добавляете новый указатель суффикса для нового node. Назначением для этого указателя суффикса будет node в сокращенной активной точке. Этот node будет либо уже существовать, либо быть создан на следующей итерации этого резервного цикла.
Примечание 3: часть канонизации просто экономит время при проверке активной точки. Например, предположим, что вы всегда использовали origin = 0 и просто изменили первый и последний. Чтобы проверить активную точку, вам нужно будет следовать дереву суффикса каждый раз по всем промежуточным узлам. Имеет смысл кэшировать результат этого пути, записывая только расстояние от последнего node.
Можете ли вы привести пример кода того, что вы подразумеваете под "фиксировать" ограничивающие переменные?
Предупреждение о безопасности: я также нашел этот алгоритм особенно трудным для понимания, поэтому, пожалуйста, поймите, что эта интуиция, вероятно, будет неправильной во всех важных деталях...
-
0В одной из научных работ термин «правильный» означает, что «правильный суффикс» строки не содержит ее первого символа. Иногда вы называете целую подстроку «суффиксом», но при определении алгоритма термины «строка», «подстрока» и «суффикс» свободно используются, и иногда вам необходимо четко понимать, что вы подразумеваете под «суффиксом», поэтому термин «надлежащий суффикс» исключает называть все это суффиксом. Таким образом, подстрока суффикса строки может быть любой допустимой подстрокой и может иметь правильный суффикс, который не является тем же суффиксом. Потому что логика.
Привет, я попытался реализовать описанную выше процедуру в рубине, пожалуйста, проверьте ее. он работает нормально.
Единственная разница в реализации заключается в том, что я попытался использовать объект edge вместо простого использования символов.
его также присутствует в https://gist.github.com/suchitpuri/9304856
require 'pry'
class Edge
attr_accessor :data , :edges , :suffix_link
def initialize data
@data = data
@edges = []
@suffix_link = nil
end
def find_edge element
self.edges.each do |edge|
return edge if edge.data.start_with? element
end
return nil
end
end
class SuffixTrees
attr_accessor :root , :active_point , :remainder , :pending_prefixes , :last_split_edge , :remainder
def initialize
@root = Edge.new nil
@active_point = { active_node: @root , active_edge: nil , active_length: 0}
@remainder = 0
@pending_prefixes = []
@last_split_edge = nil
@remainder = 1
end
def build string
string.split("").each_with_index do |element , index|
add_to_edges @root , element
update_pending_prefix element
add_pending_elements_to_tree element
active_length = @active_point[:active_length]
# if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data[0..active_length-1] == @active_point[:active_edge].data[active_length..@active_point[:active_edge].data.length-1])
# @active_point[:active_edge].data = @active_point[:active_edge].data[0..active_length-1]
# @active_point[:active_edge].edges << Edge.new(@active_point[:active_edge].data)
# end
if(@active_point[:active_edge] && @active_point[:active_edge].data && @active_point[:active_edge].data.length == @active_point[:active_length] )
@active_point[:active_node] = @active_point[:active_edge]
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0])
@active_point[:active_length] = 0
end
end
end
def add_pending_elements_to_tree element
to_be_deleted = []
update_active_length = false
# binding.pry
if( @active_point[:active_node].find_edge(element[0]) != nil)
@active_point[:active_length] = @active_point[:active_length] + 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(element[0]) if @active_point[:active_edge] == nil
@remainder = @remainder + 1
return
end
@pending_prefixes.each_with_index do |pending_prefix , index|
# binding.pry
if @active_point[:active_edge] == nil and @active_point[:active_node].find_edge(element[0]) == nil
@active_point[:active_node].edges << Edge.new(element)
else
@active_point[:active_edge] = node.find_edge(element[0]) if @active_point[:active_edge] == nil
data = @active_point[:active_edge].data
data = data.split("")
location = @active_point[:active_length]
# binding.pry
if(data[0..location].join == pending_prefix or @active_point[:active_node].find_edge(element) != nil )
else #tree split
split_edge data , index , element
end
end
end
end
def update_pending_prefix element
if @active_point[:active_edge] == nil
@pending_prefixes = [element]
return
end
@pending_prefixes = []
length = @active_point[:active_edge].data.length
data = @active_point[:active_edge].data
@remainder.times do |ctr|
@pending_prefixes << data[-(ctr+1)..data.length-1]
end
@pending_prefixes.reverse!
end
def split_edge data , index , element
location = @active_point[:active_length]
old_edges = []
internal_node = (@active_point[:active_edge].edges != nil)
if (internal_node)
old_edges = @active_point[:active_edge].edges
@active_point[:active_edge].edges = []
end
@active_point[:active_edge].data = data[0..location-1].join
@active_point[:active_edge].edges << Edge.new(data[location..data.size].join)
if internal_node
@active_point[:active_edge].edges << Edge.new(element)
else
@active_point[:active_edge].edges << Edge.new(data.last)
end
if internal_node
@active_point[:active_edge].edges[0].edges = old_edges
end
#setup the suffix link
if @last_split_edge != nil and @last_split_edge.data.end_with?@active_point[:active_edge].data
@last_split_edge.suffix_link = @active_point[:active_edge]
end
@last_split_edge = @active_point[:active_edge]
update_active_point index
end
def update_active_point index
if(@active_point[:active_node] == @root)
@active_point[:active_length] = @active_point[:active_length] - 1
@remainder = @remainder - 1
@active_point[:active_edge] = @active_point[:active_node].find_edge(@pending_prefixes.first[index+1])
else
if @active_point[:active_node].suffix_link != nil
@active_point[:active_node] = @active_point[:active_node].suffix_link
else
@active_point[:active_node] = @root
end
@active_point[:active_edge] = @active_point[:active_node].find_edge(@active_point[:active_edge].data[0])
@remainder = @remainder - 1
end
end
def add_to_edges root , element
return if root == nil
root.data = root.data + element if(root.data and root.edges.size == 0)
root.edges.each do |edge|
add_to_edges edge , element
end
end
end
suffix_tree = SuffixTrees.new
suffix_tree.build("abcabxabcd")
binding.pry
@jogojapan вы принесли удивительное объяснение и визуализацию. Но поскольку @makagonov упомянул об отсутствии некоторых правил относительно установки суффикс-ссылок. Это видно красиво, когда шаг за шагом на http://brenden.github.io/ukkonen-animation/ через слово aabaaabb. Когда вы переходите от шага 10 к шагу 11, нет суффикса связи от node 5 до node 2, но активная точка внезапно перемещается туда.
@makagonov, так как я живу в мире Java, я также попытался выполнить вашу реализацию, чтобы понять рабочий процесс ST, но мне было трудно:
- объединение ребер с узлами
- с помощью указателей указателей вместо ссылок
- разрывает утверждения;
- инструкции продолжения;
Итак, у меня появилась такая реализация на Java, которая, я надеюсь, будет более четко отражать все шаги и сократит время обучения для других людей Java:
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class ST {
public class Node {
private final int id;
private final Map<Character, Edge> edges;
private Node slink;
public Node(final int id) {
this.id = id;
this.edges = new HashMap<>();
}
public void setSlink(final Node slink) {
this.slink = slink;
}
public Map<Character, Edge> getEdges() {
return this.edges;
}
public Node getSlink() {
return this.slink;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"id\"")
.append(":")
.append(this.id)
.append(",")
.append("\"slink\"")
.append(":")
.append(this.slink != null ? this.slink.id : null)
.append(",")
.append("\"edges\"")
.append(":")
.append(edgesToString(word))
.append("}")
.toString();
}
private StringBuilder edgesToString(final String word) {
final StringBuilder edgesStringBuilder = new StringBuilder();
edgesStringBuilder.append("{");
for(final Map.Entry<Character, Edge> entry : this.edges.entrySet()) {
edgesStringBuilder.append("\"")
.append(entry.getKey())
.append("\"")
.append(":")
.append(entry.getValue().toString(word))
.append(",");
}
if(!this.edges.isEmpty()) {
edgesStringBuilder.deleteCharAt(edgesStringBuilder.length() - 1);
}
edgesStringBuilder.append("}");
return edgesStringBuilder;
}
public boolean contains(final String word, final String suffix) {
return !suffix.isEmpty()
&& this.edges.containsKey(suffix.charAt(0))
&& this.edges.get(suffix.charAt(0)).contains(word, suffix);
}
}
public class Edge {
private final int from;
private final int to;
private final Node next;
public Edge(final int from, final int to, final Node next) {
this.from = from;
this.to = to;
this.next = next;
}
public int getFrom() {
return this.from;
}
public int getTo() {
return this.to;
}
public Node getNext() {
return this.next;
}
public int getLength() {
return this.to - this.from;
}
public String toString(final String word) {
return new StringBuilder()
.append("{")
.append("\"content\"")
.append(":")
.append("\"")
.append(word.substring(this.from, this.to))
.append("\"")
.append(",")
.append("\"next\"")
.append(":")
.append(this.next != null ? this.next.toString(word) : null)
.append("}")
.toString();
}
public boolean contains(final String word, final String suffix) {
if(this.next == null) {
return word.substring(this.from, this.to).equals(suffix);
}
return suffix.startsWith(word.substring(this.from,
this.to)) && this.next.contains(word, suffix.substring(this.to - this.from));
}
}
public class ActivePoint {
private final Node activeNode;
private final Character activeEdgeFirstCharacter;
private final int activeLength;
public ActivePoint(final Node activeNode,
final Character activeEdgeFirstCharacter,
final int activeLength) {
this.activeNode = activeNode;
this.activeEdgeFirstCharacter = activeEdgeFirstCharacter;
this.activeLength = activeLength;
}
private Edge getActiveEdge() {
return this.activeNode.getEdges().get(this.activeEdgeFirstCharacter);
}
public boolean pointsToActiveNode() {
return this.activeLength == 0;
}
public boolean activeNodeIs(final Node node) {
return this.activeNode == node;
}
public boolean activeNodeHasEdgeStartingWith(final char character) {
return this.activeNode.getEdges().containsKey(character);
}
public boolean activeNodeHasSlink() {
return this.activeNode.getSlink() != null;
}
public boolean pointsToOnActiveEdge(final String word, final char character) {
return word.charAt(this.getActiveEdge().getFrom() + this.activeLength) == character;
}
public boolean pointsToTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() == this.activeLength;
}
public boolean pointsAfterTheEndOfActiveEdge() {
return this.getActiveEdge().getLength() < this.activeLength;
}
public ActivePoint moveToEdgeStartingWithAndByOne(final char character) {
return new ActivePoint(this.activeNode, character, 1);
}
public ActivePoint moveToNextNodeOfActiveEdge() {
return new ActivePoint(this.getActiveEdge().getNext(), null, 0);
}
public ActivePoint moveToSlink() {
return new ActivePoint(this.activeNode.getSlink(),
this.activeEdgeFirstCharacter,
this.activeLength);
}
public ActivePoint moveTo(final Node node) {
return new ActivePoint(node, this.activeEdgeFirstCharacter, this.activeLength);
}
public ActivePoint moveByOneCharacter() {
return new ActivePoint(this.activeNode,
this.activeEdgeFirstCharacter,
this.activeLength + 1);
}
public ActivePoint moveToEdgeStartingWithAndByActiveLengthMinusOne(final Node node,
final char character) {
return new ActivePoint(node, character, this.activeLength - 1);
}
public ActivePoint moveToNextNodeOfActiveEdge(final String word, final int index) {
return new ActivePoint(this.getActiveEdge().getNext(),
word.charAt(index - this.activeLength + this.getActiveEdge().getLength()),
this.activeLength - this.getActiveEdge().getLength());
}
public void addEdgeToActiveNode(final char character, final Edge edge) {
this.activeNode.getEdges().put(character, edge);
}
public void splitActiveEdge(final String word,
final Node nodeToAdd,
final int index,
final char character) {
final Edge activeEdgeToSplit = this.getActiveEdge();
final Edge splittedEdge = new Edge(activeEdgeToSplit.getFrom(),
activeEdgeToSplit.getFrom() + this.activeLength,
nodeToAdd);
nodeToAdd.getEdges().put(word.charAt(activeEdgeToSplit.getFrom() + this.activeLength),
new Edge(activeEdgeToSplit.getFrom() + this.activeLength,
activeEdgeToSplit.getTo(),
activeEdgeToSplit.getNext()));
nodeToAdd.getEdges().put(character, new Edge(index, word.length(), null));
this.activeNode.getEdges().put(this.activeEdgeFirstCharacter, splittedEdge);
}
public Node setSlinkTo(final Node previouslyAddedNodeOrAddedEdgeNode,
final Node node) {
if(previouslyAddedNodeOrAddedEdgeNode != null) {
previouslyAddedNodeOrAddedEdgeNode.setSlink(node);
}
return node;
}
public Node setSlinkToActiveNode(final Node previouslyAddedNodeOrAddedEdgeNode) {
return setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, this.activeNode);
}
}
private static int idGenerator;
private final String word;
private final Node root;
private ActivePoint activePoint;
private int remainder;
public ST(final String word) {
this.word = word;
this.root = new Node(idGenerator++);
this.activePoint = new ActivePoint(this.root, null, 0);
this.remainder = 0;
build();
}
private void build() {
for(int i = 0; i < this.word.length(); i++) {
add(i, this.word.charAt(i));
}
}
private void add(final int index, final char character) {
this.remainder++;
boolean characterFoundInTheTree = false;
Node previouslyAddedNodeOrAddedEdgeNode = null;
while(!characterFoundInTheTree && this.remainder > 0) {
if(this.activePoint.pointsToActiveNode()) {
if(this.activePoint.activeNodeHasEdgeStartingWith(character)) {
activeNodeHasEdgeStartingWithCharacter(character, previouslyAddedNodeOrAddedEdgeNode);
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
rootNodeHasNotEdgeStartingWithCharacter(index, character);
}
else {
previouslyAddedNodeOrAddedEdgeNode = internalNodeHasNotEdgeStartingWithCharacter(index,
character, previouslyAddedNodeOrAddedEdgeNode);
}
}
}
else {
if(this.activePoint.pointsToOnActiveEdge(this.word, character)) {
activeEdgeHasCharacter();
characterFoundInTheTree = true;
}
else {
if(this.activePoint.activeNodeIs(this.root)) {
previouslyAddedNodeOrAddedEdgeNode = edgeFromRootNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
else {
previouslyAddedNodeOrAddedEdgeNode = edgeFromInternalNodeHasNotCharacter(index,
character,
previouslyAddedNodeOrAddedEdgeNode);
}
}
}
}
}
private void activeNodeHasEdgeStartingWithCharacter(final char character,
final Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByOne(character);
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private void rootNodeHasNotEdgeStartingWithCharacter(final int index, final char character) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
this.activePoint = this.activePoint.moveTo(this.root);
this.remainder--;
assert this.remainder == 0;
}
private Node internalNodeHasNotEdgeStartingWithCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
this.activePoint.addEdgeToActiveNode(character, new Edge(index, this.word.length(), null));
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkToActiveNode(previouslyAddedNodeOrAddedEdgeNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private void activeEdgeHasCharacter() {
this.activePoint = this.activePoint.moveByOneCharacter();
if(this.activePoint.pointsToTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
private Node edgeFromRootNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
this.activePoint = this.activePoint.moveToEdgeStartingWithAndByActiveLengthMinusOne(this.root,
this.word.charAt(index - this.remainder + 2));
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private Node edgeFromInternalNodeHasNotCharacter(final int index,
final char character,
Node previouslyAddedNodeOrAddedEdgeNode) {
final Node newNode = new Node(idGenerator++);
this.activePoint.splitActiveEdge(this.word, newNode, index, character);
previouslyAddedNodeOrAddedEdgeNode = this.activePoint.setSlinkTo(previouslyAddedNodeOrAddedEdgeNode, newNode);
if(this.activePoint.activeNodeHasSlink()) {
this.activePoint = this.activePoint.moveToSlink();
}
else {
this.activePoint = this.activePoint.moveTo(this.root);
}
this.activePoint = walkDown(index);
this.remainder--;
return previouslyAddedNodeOrAddedEdgeNode;
}
private ActivePoint walkDown(final int index) {
while(!this.activePoint.pointsToActiveNode()
&& (this.activePoint.pointsToTheEndOfActiveEdge() || this.activePoint.pointsAfterTheEndOfActiveEdge())) {
if(this.activePoint.pointsAfterTheEndOfActiveEdge()) {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge(this.word, index);
}
else {
this.activePoint = this.activePoint.moveToNextNodeOfActiveEdge();
}
}
return this.activePoint;
}
public String toString(final String word) {
return this.root.toString(word);
}
public boolean contains(final String suffix) {
return this.root.contains(this.word, suffix);
}
public static void main(final String[] args) {
final String[] words = {
"abcabcabc$",
"abc$",
"abcabxabcd$",
"abcabxabda$",
"abcabxad$",
"aabaaabb$",
"aababcabcd$",
"ababcabcd$",
"abccba$",
"mississipi$",
"abacabadabacabae$",
"abcabcd$",
"00132220$"
};
Arrays.stream(words).forEach(word -> {
System.out.println("Building suffix tree for word: " + word);
final ST suffixTree = new ST(word);
System.out.println("Suffix tree: " + suffixTree.toString(word));
for(int i = 0; i < word.length() - 1; i++) {
assert suffixTree.contains(word.substring(i)) : word.substring(i);
}
});
}
}
Ещё вопросы
- 1динамические события Google Analytics на основе события диспетчера тегов
- 0создание столбцов и строк; запрашивая количество строк, которые пользователь хочет вывести на дисплей,
- 1В папке классов внутри войны классов не найдено
- 0Холст различной формы с плагином fabricjs
- 0Как я могу добавить переменную php в javascript?
- 1Теория позади изображения вычитает 0,5, а затем умножает на 2
- 0Как отсортировать набор по разыменованным значениям? [Дубликат]
- 0Как зарегистрировать новый модуль в Zend Framework 2
- 1Почему для запуска функции требуется первый двойной щелчок, а затем один щелчок?
- 0Не удалось установить соединение с Pphmyadmin с помощью «hp_network_getaddresses: getaddrinfo fail»
- 0Как переименовать ссылки с вопросительным знаком?
- 1Импорт .txt файла с запятыми и без пробелов между числами
- 0массивы javascript внутри массива
- 1Ошибка: не указан путь к программе JavaScript
- 1Сортировать список по имени, дате и иерархии
- 0Пользовательский интерфейс jQuery, сбрасываемый за пределы видимой области jScrollpane, ловит событие удаления
- 1Как убрать черную полосу, появляющуюся внизу?
- 0Создание эскиза изображения из видео не работает
- 0Код для блокировки клавиатуры и мыши
- 1Управление отображением потокового PDF в браузере
- 0Передать параметр в функцию контроллера Angularjs из директивы
- 1Неявное EMAIL Intent Android; работает БЕЗ ФИЛЬТРА
- 1gridworld помогают движущимся твари открыть место
- 0На моей доске объявлений PHP, как я могу вывести изображение в соответствии с соответствующим постом?
- 0Чтение еще одной строки при разборе CSV в PHP
- 0Неправильная фильтрация списка, созданного с помощью ng-repeat (AngularJS)
- 1NullPointException и длина массива объектов
- 0Почему .NET 4.0 скрывает атрибут имени в созданном LinkButton?
- 1Как рассчитать выход нейронной сети?
- 0Xampp - завершение работы MySql - не работает
- 0MessageBox Threading Проблемы
- 1Office 365 надстройка Javascript - синтез речи
- 3Интеллидж андроид проект. Gradle 5.2.1. Причина: java.util.ConcurrentModificationException
- 1javax.naming.NameNotFoundException: имя [SessionFactory] не связано в этом контексте. Невозможно найти [SessionFactory]
- 0Как я могу заполнить HTML-таблицу из локального текстового файла?
- 0Как выбрать в MySQL данные | xx | xx | xx |
- 0Почему метод setUserId не работает в сущности symfony2?
- 0мы можем использовать скомпилированный код hiphop на производственном сервере без исходного кода?
- 1Страница входа с использованием Mvvmcross
- 0Ожидаемый возврат алгоритма поиска STL
- 1Как сделать v-for итерацию в определенном порядке?
- 1Применить цвет к определенному слову в строке
- 1Android Retrofit2 / RxJava2 / Room - Простая обработка данных
- 1double.ToString («G»), но всегда включать точку?
- 0Запустите .exe файл кода C, используя Eclipse
- 1AccessViolationException при добавлении элемента в список
- 1Подсчитать количество каждого символа в строке
- 1Как начать потоковое видео с помощью webRTC?
- 0JQuery закрыть диалоговое окно, когда завершение вызова AJAX
