Числа Фибоначчи, с однострочником в Python 3?

Редко встречающийся трюк заключается в том, что лямбда-функция может ссылаться на себя рекурсивно:

fib = lambda n: n if n < 2 else fib(n-1) + fib(n-2)

Кстати, он редко встречается, потому что он запутан, и в этом случае он также неэффективен. Это гораздо лучше написать на нескольких строках:

def fibs():
    a = 0
    b = 1
    while True:
        yield a
        a, b = b, a + b

Недавно я узнал об использовании матричного умножения для генерации чисел Фибоначчи, что было довольно круто. Вы берете базовую матрицу:

[1, 1]
[1, 0]

и умножить его на N раз, чтобы получить:

[F(N+1), F(N)]
[F(N), F(N-1)]

Сегодня утром, размышляя в паре на душевой стене, я понял, что вы можете сократить время работы пополам, начиная со второй матрицы и умножить ее на себя N/2 раза, затем используя N, чтобы выбрать индекс из первой строки/столбца.

С небольшим сжатием я получил его до одной строки:

import numpy

def mm_fib(n):
    return (numpy.matrix([[2,1],[1,1]])**(n//2))[0,(n+1)%2]

>>> [mm_fib(i) for i in range(20)]
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181]

Если мы считаем, что "самый Pythonic way" будет изящным и эффективным, тогда:

def fib(nr):
    return int(((1 + math.sqrt(5)) / 2) ** nr / math.sqrt(5) + 0.5)

побеждает. Зачем использовать неэффективный алгоритм (и если вы начнете использовать memoization, мы можем забыть о oneliner), когда вы можете решить проблему просто отлично в O (1) путем аппроксимации результата с золотым соотношением? Хотя на самом деле я, очевидно, написал бы его в этой форме:

def fib(nr):
    ratio = (1 + math.sqrt(5)) / 2
    return int(ratio ** nr / math.sqrt(5) + 0.5)

Более эффективный и намного понятный.

Это нерекурсивный (анонимный) memoizing one liner

fib = lambda x,y=[1,1]:([(y.append(y[-1]+y[-2]),y[-1])[1] for i in range(1+x-len(y))],y[x])[1]

fib = lambda n, x=0, y=1 : x if not n else fib(n-1, y, x+y)

время выполнения O (n), fib (0) = 0, fib (1) = 1, fib (2) = 1...

Это замкнутое выражение для ряда Фибоначчи, которое использует целочисленную арифметику и достаточно эффективно.

fib = lambda n:pow(2<<n,n+1,(4<<2*n)-(2<<n)-1)%(2<<n)

>> fib(1000)
4346655768693745643568852767504062580256466051737178
0402481729089536555417949051890403879840079255169295
9225930803226347752096896232398733224711616429964409
06533187938298969649928516003704476137795166849228875L

Он вычисляет результат в арифметических операциях O (log n), каждый из которых действует на целые числа с O (n) битами. Учитывая, что результатом (n-е число Фибоначчи) является O (n) бит, метод вполне разумный.

На основе genefib4 из http://fare.tunes.org/files/fun/fibonacci.lisp, который, в свою очередь, был основан на менее эффективном замкнутом выражении, (см.: http://paulhankin.github.io/Fibonacci/)

Другой пример, отвечая на отзыв от Марка Байерса:

fib = lambda n,a=0,b=1: a if n<=0 else fib(n-1,b,a+b)

Здесь реализована реализация, которая не использует рекурсию, и только запоминает последние два значения вместо всей истории последовательности.

nthfib() ниже - прямое решение исходной задачи (до тех пор, пока импорт разрешен)

Это менее изящно, чем использование методов "Уменьшить" выше, но, хотя и немного отличается от того, что было предложено, он получает возможность более эффективно использоваться в качестве бесконечного генератора, если нужно вывести последовательность до n-го числа (переписывая немного как волокно() ниже).

from itertools import imap, islice, repeat

nthfib = lambda n: next(islice((lambda x=[0, 1]: imap((lambda x: (lambda setx=x.__setitem__, x0_temp=x[0]: (x[1], setx(0, x[1]), setx(1, x0_temp+x[1]))[0])()), repeat(x)))(), n-1, None))    

>>> nthfib(1000)
43466557686937456435688527675040625802564660517371780402481729089536555417949051
89040387984007925516929592259308032263477520968962323987332247116164299644090653
3187938298969649928516003704476137795166849228875L

from itertools import imap, islice, repeat

fibgen = lambda:(lambda x=[0,1]: imap((lambda x: (lambda setx=x.__setitem__, x0_temp=x[0]: (x[1], setx(0, x[1]), setx(1, x0_temp+x[1]))[0])()), repeat(x)))()

>>> list(islice(fibgen(),12))
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144]

Я новичок в Python, но сделал некоторые меры в учебных целях. Я собрал некоторый алгоритм Фибо и принял некоторые меры.

from datetime import datetime
import matplotlib.pyplot as plt
from functools import wraps
from functools import reduce
from functools import lru_cache
import numpy


def time_it(f):

    @wraps(f)
    def wrapper(*args, **kwargs):
        start_time = datetime.now()

        f(*args, **kwargs)

        end_time = datetime.now()
        elapsed = end_time - start_time
        elapsed = elapsed.microseconds

        return elapsed
    return wrapper


@time_it
def fibslow(n):
    if n <= 1:
        return n

    else:
        return fibslow(n-1) + fibslow(n-2)


@time_it
@lru_cache(maxsize=10)
def fibslow_2(n):
    if n <= 1:
        return n

    else:
        return fibslow_2(n-1) + fibslow_2(n-2)


@time_it
def fibfast(n):
    if n <= 1:
        return n

    a, b = 0, 1

    for i in range(1, n+1):
        a, b = b, a + b

    return a


@time_it
def fib_reduce(n):
    return reduce(lambda x, n: [x[1], x[0]+x[1]], range(n), [0, 1])[0]


@time_it
def mm_fib(n):
    return (numpy.matrix([[2, 1], [1, 1]])**(n//2))[0, (n+1) % 2]


@time_it
def fib_ia(n):
    return pow(2 << n, n+1, (4 << 2 * n) - (2 << n)-1) % (2 << n)


if __name__ == '__main__':

    X = range(1, 200)
#    fibslow_times = [fibslow(i) for i in X]
    fibslow_2_times = [fibslow_2(i) for i in X]
    fibfast_times = [fibfast(i) for i in X]
    fib_reduce_times = [fib_reduce(i) for i in X]
    fib_mm_times = [mm_fib(i) for i in X]
    fib_ia_times = [fib_ia(i) for i in X]

#    print(fibslow_times)
#    print(fibfast_times)
#    print(fib_reduce_times)

    plt.figure()
#    plt.plot(X, fibslow_times, label='Slow Fib')
    plt.plot(X, fibslow_2_times, label='Slow Fib w cache')
    plt.plot(X, fibfast_times, label='Fast Fib')
    plt.plot(X, fib_reduce_times, label='Reduce Fib')
    plt.plot(X, fib_mm_times, label='Numpy Fib')
    plt.plot(X, fib_ia_times, label='Fib ia')
    plt.xlabel('n')
    plt.ylabel('time (microseconds)')
    plt.legend()
    plt.show()

Результат обычно одинаков.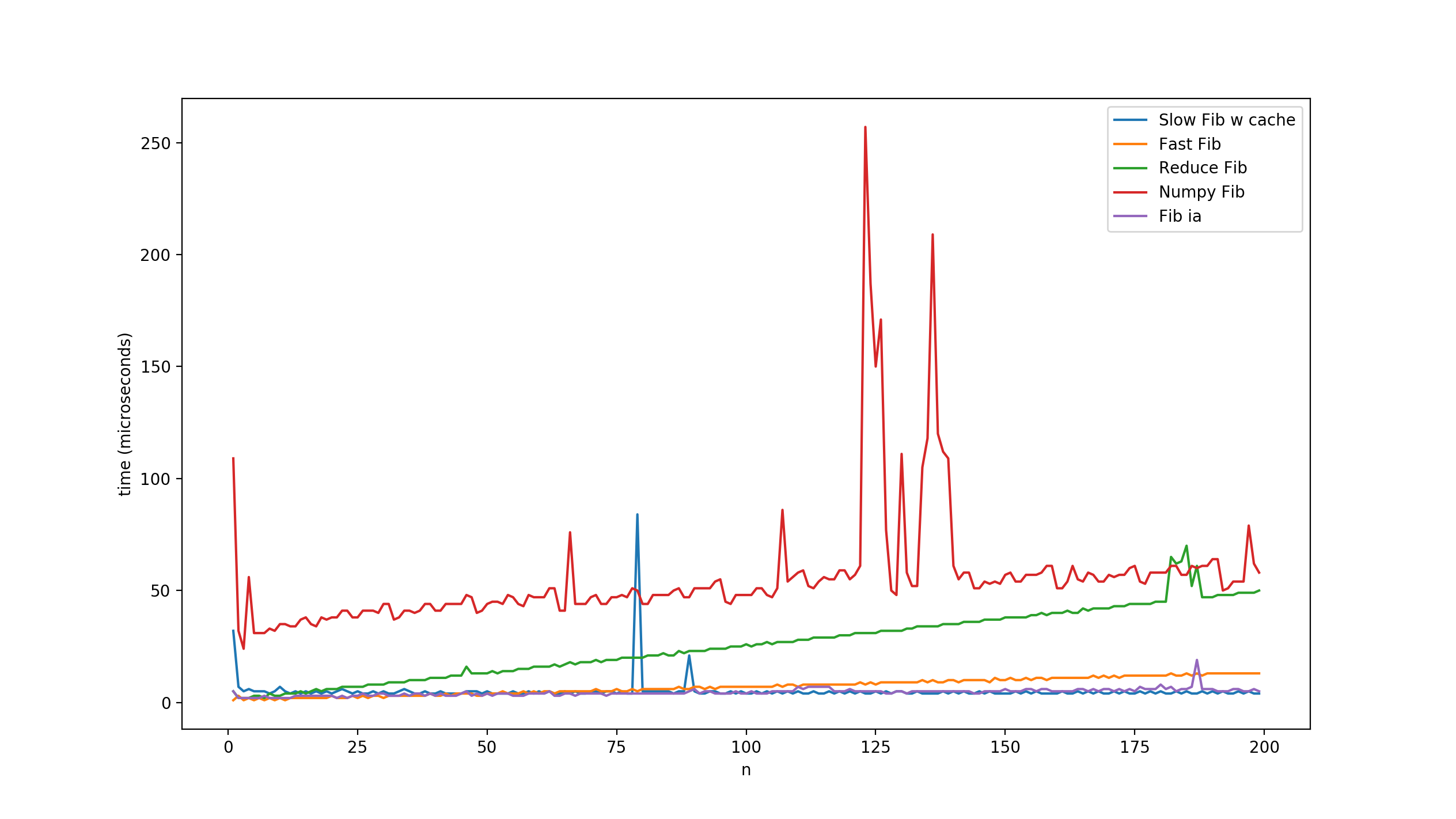

Fiboslow_2 с рекурсией и кешем, целочисленная арифметика Fib и алгоритмы Fibfast кажутся лучшими. Возможно, мой декоратор не лучшая вещь для измерения производительности, но для обзора это показалось хорошим.

Почему бы не использовать понимание списка?

from math import sqrt, floor
[floor(((1+sqrt(5))**n-(1-sqrt(5))**n)/(2**n*sqrt(5))) for n in range(100)]

Без математического импорта, но менее симпатичного:

[int(((1+(5**0.5))**n-(1-(5**0.5))**n)/(2**n*(5**0.5))) for n in range(100)]

Мои 2 цента

# One Liner
def nthfibonacci(n):
    return long(((((1+5**.5)/2)**n)-(((1-5**.5)/2)**n))/5**.5)

ИЛИ

# Steps
def nthfibonacci(nth):
    sq5 = 5**.5
    phi1 = (1+sq5)/2
    phi2 = -1 * (phi1 -1)
    n1 = phi1**(nth+1)
    n2 = phi2**(nth+1)
    return long((n1 - n2)/sq5)

Я не знаю, является ли это самым питоническим методом, но это лучшее, что я мог бы придумать: →

Fibonacci = lambda x,y=[1,1]:[1]*x if (x<2) else ([y.append(y[q-1] + y[q-2]) for q in range(2,x)],y)[1]

В приведенном выше коде не используется рекурсия, просто список для хранения значений.

def fib(n):
    x =[0,1]
    for i in range(n):
        x=[x[1],x[0]+x[1]]
    return x[0]

возьмите реплику от Джейсона С, я думаю, что моя версия имеет лучшее понимание.

Чтобы решить эту проблему, я был вдохновлен аналогичным вопросом здесь, в Stackoverflow Single Statement Fibonacci, и я получил эту единственную функцию, которая может вывести список последовательности фибоначчи, Хотя это Python 2 script, не проверенный на Python 3:

(lambda n, fib=[0,1]: fib[:n]+[fib.append(fib[-1] + fib[-2]) or fib[-1] for i in range(n-len(fib))])(10)

назначьте эту лямбда-функцию переменной, чтобы ее повторно использовать:

fib = (lambda n, fib=[0,1]: fib[:n]+[fib.append(fib[-1] + fib[-2]) or fib[-1] for i in range(n-len(fib))])
fib(10)

output - это список последовательности фибоначчи:

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

Начиная с Python 3.8 и введением выражений присваивания (PEP 572) (:= оператор), мы можем использовать и обновлять переменную в пределах понимания списка:

fib = lambda n,x=(0,1):[x := (x[1], sum(x)) for i in range(n+1)][-1][0]

Это:

• Инициирует дуэт n-1 и n-2 как кортеж x=(0, 1)
• Как часть циклического осмысления списка n раз, x обновляется через выражение присваивания (x := (x[1], sum(x))) для новых значений n-1 и n-2
• Наконец, мы возвращаемся из последней итерации, первой части x

Вы можете сгенерировать один раз список с некоторыми значениями и использовать по мере необходимости:

fib_fix = []

fib = lambda x: 1 if x <=2 else fib_fix[x-3] if x-2 <= len(fib_fix) else (fib_fix.append(fib(x-2) + fib(x-1)) or fib_fix[-1])

fib_x = lambda x: [fib(n) for n in range(1,x+1)]

fib_100 = fib_x(100)

чем, например:

a = fib_fix[76]

вот как я это делаю, однако функция возвращает None для части строки распознавания списка, чтобы позволить мне вставить цикл внутри. поэтому в основном это то, что он добавляет новые элементы fib seq внутри списка, который состоит из двух элементов

>>f=lambda list,x :print('The list must be of 2 or more') if len(list)<2 else [list.append(list[-1]+list[-2]) for i in range(x)]
>>a=[1,2]
>>f(a,7)

Лямбда с логическими операторами

fibonacci_oneline = lambda n = 10, out = []: [ out.append(i) or i if i <= 1 else out.append(out[-1] + out[-2]) or out[-1] for i in range(n)]

Простой генератор чисел Фибоначчи с использованием рекурсии

fib = lambda x: 1-x if x < 2 else  fib(x-1)+fib(x-2)
print fib(100)

Это занимает время, чтобы вычислить fib(100) на моем компьютере.

Существует также закрытая форма чисел Фибоначчи.

fib = lambda n: int(1/sqrt(5)*((1+sqrt(5))**n-(1-sqrt(5))**n)/2**n)
print fib(50)

Это работает почти до 72 номеров из-за проблемы с точностью.

Similar:

    def fibonacci(n):
      f=[1]+[0]
      for i in range(n):
        f=[sum(f)] + f[:-1]
      print f[1]