Более быстрый способ инициализации массивов с помощью умножения пустых матриц? (Matlab)
Я наткнулся на странный способ (на мой взгляд), что Matlab имеет дело с пустыми матрицами. Например, если две пустые матрицы умножаются, результат:
zeros(3,0)*zeros(0,3)
ans =
0 0 0
0 0 0
0 0 0
Теперь это уже застало меня врасплох, однако быстрый поиск привлек меня к ссылке выше, и я получил объяснение несколько искаженной логики, почему это происходит.
Однако, ничто не подготовило меня к следующему наблюдению. Я спросил себя: насколько эффективен этот тип умножения и просто используется функция zeros(n), например, для инициализации? Я использовал timeit, чтобы ответить на это:
f=@() zeros(1000)
timeit(f)
ans =
0.0033
против
g=@() zeros(1000,0)*zeros(0,1000)
timeit(g)
ans =
9.2048e-06
Оба имеют одинаковый результат матрицы 1000x1000 нулей класса double, но пустая матрица умножается на ~ 350 раз быстрее! (аналогичный результат происходит с использованием tic и toc и цикла)
Как это может быть? timeit или tic,toc блеф или я нашел более быстрый способ инициализации матриц?
(это было сделано с помощью matlab 2012a, на машине win7-64, intel-i5 650 3.2Ghz...)
EDIT:
После прочтения ваших отзывов я более тщательно рассмотрел эту особенность и протестировал на двух разных компьютерах (тот же самый matlab ver, хотя 2012a) код, который проверяет время выполнения и размер матрицы n. Это то, что я получаю:
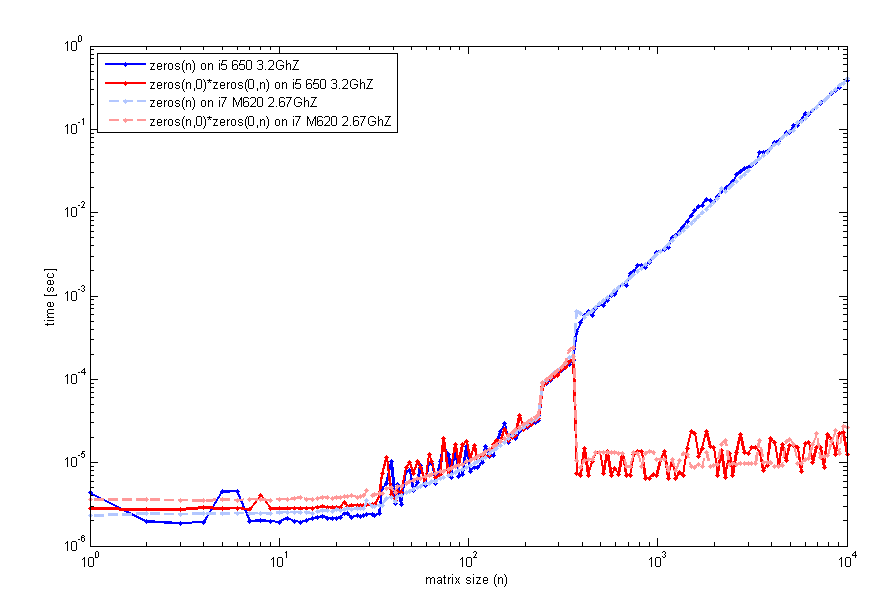
Код для генерации этого используемого timeit, как и раньше, но цикл с tic и toc будет выглядеть одинаково. Таким образом, для небольших размеров zeros(n) сравнимо. Однако вокруг n=400 наблюдается скачок производительности для пустого матричного умножения. Код, который я использовал для создания этого сюжета, был:
n=unique(round(logspace(0,4,200)));
for k=1:length(n)
f=@() zeros(n(k));
t1(k)=timeit(f);
g=@() zeros(n(k),0)*zeros(0,n(k));
t2(k)=timeit(g);
end
loglog(n,t1,'b',n,t2,'r');
legend('zeros(n)','zeros(n,0)*zeros(0,n)',2);
xlabel('matrix size (n)'); ylabel('time [sec]');
Вы тоже испытываете это?
РЕДАКТИРОВАТЬ № 2:
Кстати, пустое матричное умножение не требуется для получения этого эффекта. Можно просто сделать:
z(n,n)=0;
где n > некоторый пороговый размер матрицы, рассматриваемый на предыдущем графике, и получить профиль эффективности точный, как с пустым умножением матрицы (снова используя timeit).
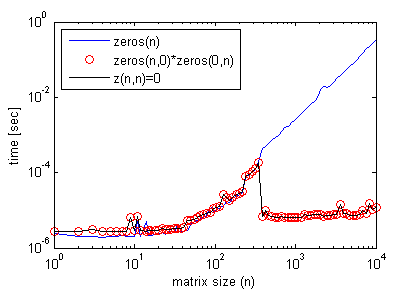
Здесь пример, где он повышает эффективность кода:
n = 1e4;
clear z1
tic
z1 = zeros( n );
for cc = 1 : n
z1(:,cc)=cc;
end
toc % Elapsed time is 0.445780 seconds.
%%
clear z0
tic
z0 = zeros(n,0)*zeros(0,n);
for cc = 1 : n
z0(:,cc)=cc;
end
toc % Elapsed time is 0.297953 seconds.
Однако использование z(n,n)=0; приводит к аналогичным результатам в случае zeros(n).
-
0@natan, вы также можете попробовать произведение Кронекера на нулевые матрицы. Как-то это может быть даже квадратично быстро.Acorbe
-
2@natan - если вы собираетесь создавать записи вики-тегов, такие как эта , копируя и вставляя дословно из Википедии, пожалуйста, включите указание источника в конце вики; в противном случае вы плагиат текста .LittleBobbyTables
5 ответов
Это странно, я вижу, что f быстрее, а g медленнее, чем вы видите. Но оба они одинаковы для меня. Возможно, другая версия MATLAB?
>> g = @() zeros(1000, 0) * zeros(0, 1000);
>> f = @() zeros(1000)
f =
@()zeros(1000)
>> timeit(f)
ans =
8.5019e-04
>> timeit(f)
ans =
8.4627e-04
>> timeit(g)
ans =
8.4627e-04
РЕДАКТИРОВАТЬ, вы можете добавить + 1 для конца f и g и посмотреть, сколько времени вы получаете.
EDIT 6 января 2013 г. 7:42 EST
Я использую машину удаленно, поэтому извините за низкокачественные графики (их нужно было скрыть).
Конфигурация машины:
i7 920. 2.653 ГГц. Linux. 12 ГБ оперативной памяти. Кеш 8 МБ.
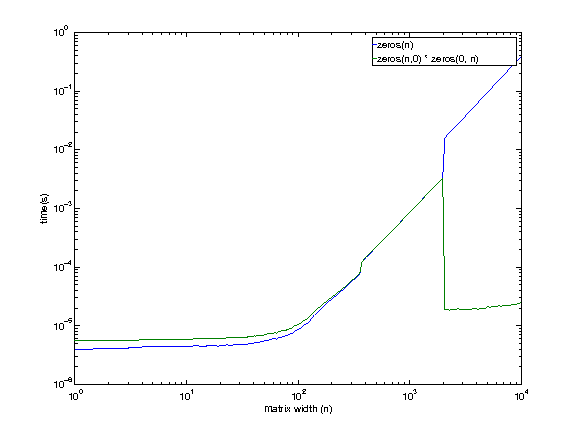
Похоже, что даже машина, к которой у меня есть доступ, показывает это поведение, за исключением большего размера (где-то между 1979 и 2073 годами). Нет причин, по которым я могу сейчас думать о том, что пустая матрица умножается быстрее при больших размерах.
Я буду изучать немного больше, прежде чем возвращаться.
РЕДАКТИРОВАТЬ 11 января 2013 г.
После сообщения @EitanT я хотел немного поработать. Я написал некоторый C-код, чтобы увидеть, как Matlab может создавать матрицу нулей. Вот код С++, который я использовал.
int main(int argc, char **argv)
{
for (int i = 1975; i <= 2100; i+=25) {
timer::start();
double *foo = (double *)malloc(i * i * sizeof(double));
for (int k = 0; k < i * i; k++) foo[k] = 0;
double mftime = timer::stop();
free(foo);
timer::start();
double *bar = (double *)malloc(i * i * sizeof(double));
memset(bar, 0, i * i * sizeof(double));
double mmtime = timer::stop();
free(bar);
timer::start();
double *baz = (double *)calloc(i * i, sizeof(double));
double catime = timer::stop();
free(baz);
printf("%d, %lf, %lf, %lf\n", i, mftime, mmtime, catime);
}
}
Вот результаты.
$ ./test
1975, 0.013812, 0.013578, 0.003321
2000, 0.014144, 0.013879, 0.003408
2025, 0.014396, 0.014219, 0.003490
2050, 0.014732, 0.013784, 0.000043
2075, 0.015022, 0.014122, 0.000045
2100, 0.014606, 0.014480, 0.000045
Как вы можете видеть, calloc (4-й столбец) кажется самым быстрым методом. Он также значительно ускоряется между 2025 и 2050 годами (предположим, это примерно в 2048 году?).
Теперь я вернулся в Matlab, чтобы проверить то же самое. Вот результаты.
>> test
1975, 0.003296, 0.003297
2000, 0.003377, 0.003385
2025, 0.003465, 0.003464
2050, 0.015987, 0.000019
2075, 0.016373, 0.000019
2100, 0.016762, 0.000020
Похоже, что как f(), так и g() используют calloc при меньших размерах (< 2048?). Но при больших размерах f() (нули (m, n)) начинает использовать malloc + memset, а g() (zeros (m, 0) * zeros (0, n)) продолжает использовать calloc.
Таким образом, расхождение объясняется следующим
- zeros (..) начинает использовать другую (более медленную?) схему при больших размерах.
-
callocтакже ведет себя несколько неожиданно, что приводит к улучшению производительности.
Это поведение в Linux. Может ли кто-то сделать тот же эксперимент на другой машине (и, возможно, в другой ОС) и посмотреть, есть ли эксперимент?
-
0Я использую Matlab 2012a на Win7-64 (на intel-i5 650 3.2Ghz), добавленный к моему вопросу) Когда я добавляю +1, я получаю, что
gмедленнее, чемfпочти в 2 раза! ... ммм -
0У меня есть старый matlab с i7 920. Возможно, в последних версиях mathworks реализовал какую-то ленивую оценку. где вывод g фактически не рассчитывается, пока это не требуется. добавление + 1 заставляет его генерировать матрицу.
Результаты могут быть немного обманчивыми. Когда вы умножаете две пустые матрицы, результирующая матрица не сразу "распределяется" и "инициализируется", скорее это откладывается до тех пор, пока вы ее сначала не используете (вроде как ленивая оценка).
То же самое относится к indexing за пределами вырасти переменную, которая в случае числовых массивов заполняет любые отсутствующие записи нулями (я потом обсужу нечисловой случай). Конечно, рост матрицы таким образом не перезаписывает существующие элементы.
Таким образом, хотя это может показаться более быстрым, вы просто задерживаете время распределения, пока вы на самом деле не начнете использовать матрицу. В конце вы будете иметь аналогичные тайминги, как если бы вы сделали выделение с самого начала.
Пример, чтобы показать это поведение, по сравнению с несколькими другими альтернативами:
N = 1000;
clear z
tic, z = zeros(N,N); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z = zeros(N,0)*zeros(0,N); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z(N,N) = 0; toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z = full(spalloc(N,N,0)); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z(1:N,1:N) = 0; toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
val = 0;
tic, z = val(ones(N)); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
clear z
tic, z = repmat(0, [N N]); toc
tic, z = z + 1; toc
assert(isequal(z,ones(N)))
Результат показывает, что если вы суммируете прошедшее время для обеих команд в каждом случае, вы получите аналогичные общие тайминги:
// zeros(N,N)
Elapsed time is 0.004525 seconds.
Elapsed time is 0.000792 seconds.
// zeros(N,0)*zeros(0,N)
Elapsed time is 0.000052 seconds.
Elapsed time is 0.004365 seconds.
// z(N,N) = 0
Elapsed time is 0.000053 seconds.
Elapsed time is 0.004119 seconds.
Другие тайминги:
// full(spalloc(N,N,0))
Elapsed time is 0.001463 seconds.
Elapsed time is 0.003751 seconds.
// z(1:N,1:N) = 0
Elapsed time is 0.006820 seconds.
Elapsed time is 0.000647 seconds.
// val(ones(N))
Elapsed time is 0.034880 seconds.
Elapsed time is 0.000911 seconds.
// repmat(0, [N N])
Elapsed time is 0.001320 seconds.
Elapsed time is 0.003749 seconds.
Эти измерения слишком малы в миллисекундах и могут быть не очень точными, поэтому вы можете запускать эти команды в цикле несколько тысяч раз и принимать среднее значение. Также иногда выполнение сохраненных M-функций выполняется быстрее, чем запуск сценариев или командную строку, так как определенные оптимизации происходят только так...
В любом случае выделение обычно выполняется один раз, поэтому кому это нужно, если требуется дополнительные 30 мс:)
Аналогичное поведение можно наблюдать с массивами ячеек или массивами структур. Рассмотрим следующий пример:
N = 1000;
tic, a = cell(N,N); toc
tic, b = repmat({[]}, [N,N]); toc
tic, c{N,N} = []; toc
который дает:
Elapsed time is 0.001245 seconds.
Elapsed time is 0.040698 seconds.
Elapsed time is 0.004846 seconds.
Обратите внимание, что даже если все они равны, они занимают различный объем памяти:
>> assert(isequal(a,b,c))
>> whos a b c
Name Size Bytes Class Attributes
a 1000x1000 8000000 cell
b 1000x1000 112000000 cell
c 1000x1000 8000104 cell
На самом деле ситуация здесь немного сложнее, так как MATLAB, вероятно, разделяет ту же пустую матрицу для всех ячеек, а не создание нескольких копий.
Массив ячеек a на самом деле представляет собой массив неинициализированных ячеек (массив NULL-указателей), а b - это массив ячеек, где каждая ячейка представляет собой пустой массив [] (внутри и из-за совместного использования данных, только первая ячейка b{1} указывает на [], а все остальные имеют ссылку на первую ячейку). Конечный массив c похож на a (неинициализированные ячейки), но с последним, содержащим пустую числовую матрицу [].
Я просмотрел список экспортированных функций C из libmx.dll (используя инструмент Dependency Walker), и я нашел несколько интересных вещи.
-
существуют недокументированные функции для создания неинициализированных массивов:
mxCreateUninitDoubleMatrix,mxCreateUninitNumericArrayиmxCreateUninitNumericMatrix. Фактически есть представление о File Exchange использует эти функции, чтобы обеспечить более быструю альтернативу функцииzeros. -
существует недокументированная функция, называемая
mxFastZeros. Googling онлайн, я могу видеть, что вы перекрестно поставили этот вопрос на MATLAB Answers, а также отличные ответы там. Джеймс Турса (тот же автор UNINIT из ранее) дал пример о том, как использовать эту недокументированную функцию. -
libmx.dllсвязан сtbbmalloc.dllразделяемой библиотекой. Это масштабируемый распределитель памяти Intel TBB. Эта библиотека обеспечивает эквивалентные функции выделения памяти (malloc,calloc,free), оптимизированные для параллельных приложений. Помните, что многие функции MATLAB автоматически многопоточны, поэтому я не удивлюсь, еслиzeros(..)многопоточно и использует распределитель памяти Intel, как только размер матрицы достаточно велик (вот недавний комментарий Loren Shure, который подтверждает этот факт).
Что касается последнего пункта о распределителе памяти, вы можете написать аналогичный тест в C/С++, подобный тому, что было @PavanYalamanchili, и сравнить доступные распределители. Что-то вроде this. Помните, что MEX файлы имеют несколько более высокое управление памятьюнакладные расходы, поскольку MATLAB автоматически освобождает любую память, которая была выделена в MEX файлах, используя функции mxCalloc, mxMalloc или mxRealloc. Для того, что стоило, в более старых версиях раньше можно было изменить внутренний менеджер памяти.
EDIT:
Вот более тщательный критерий для сравнения обсуждаемых альтернатив. В нем конкретно показано, что, как только вы подчеркиваете использование всей выделенной матрицы, все три метода находятся на равной основе, а разница незначительна.
function compare_zeros_init()
iter = 100;
for N = 512.*(1:8)
% ZEROS(N,N)
t = zeros(iter,3);
for i=1:iter
clear z
tic, z = zeros(N,N); t(i,1) = toc;
tic, z(:) = 9; t(i,2) = toc;
tic, z = z + 1; t(i,3) = toc;
end
fprintf('N = %4d, ZEROS = %.9f\n', N, mean(sum(t,2)))
% z(N,N)=0
t = zeros(iter,3);
for i=1:iter
clear z
tic, z(N,N) = 0; t(i,1) = toc;
tic, z(:) = 9; t(i,2) = toc;
tic, z = z + 1; t(i,3) = toc;
end
fprintf('N = %4d, GROW = %.9f\n', N, mean(sum(t,2)))
% ZEROS(N,0)*ZEROS(0,N)
t = zeros(iter,3);
for i=1:iter
clear z
tic, z = zeros(N,0)*zeros(0,N); t(i,1) = toc;
tic, z(:) = 9; t(i,2) = toc;
tic, z = z + 1; t(i,3) = toc;
end
fprintf('N = %4d, MULT = %.9f\n\n', N, mean(sum(t,2)))
end
end
Ниже приведены интервалы времени, усредненные по 100 итерациям с точки зрения увеличения размера матрицы. Я выполнил тесты в R2013a.
>> compare_zeros_init
N = 512, ZEROS = 0.001560168
N = 512, GROW = 0.001479991
N = 512, MULT = 0.001457031
N = 1024, ZEROS = 0.005744873
N = 1024, GROW = 0.005352638
N = 1024, MULT = 0.005359236
N = 1536, ZEROS = 0.011950846
N = 1536, GROW = 0.009051589
N = 1536, MULT = 0.008418878
N = 2048, ZEROS = 0.012154002
N = 2048, GROW = 0.010996315
N = 2048, MULT = 0.011002169
N = 2560, ZEROS = 0.017940950
N = 2560, GROW = 0.017641046
N = 2560, MULT = 0.017640323
N = 3072, ZEROS = 0.025657999
N = 3072, GROW = 0.025836506
N = 3072, MULT = 0.051533432
N = 3584, ZEROS = 0.074739924
N = 3584, GROW = 0.070486857
N = 3584, MULT = 0.072822335
N = 4096, ZEROS = 0.098791732
N = 4096, GROW = 0.095849788
N = 4096, MULT = 0.102148452
-
0спасибо Amro за подробный ответ (+1). Почему, хотя я получаю лучшую производительность, когда использую предварительное распределение пустой матрицы, как видно во втором редактировании моего вопроса? В этом примере и предварительно определяется матрица нулей, и присваиваются значения, и при этом умножение пустой матрицы побеждает обычные
zeros. Кроме того, мне нужно предварительно выделить ~ 100 раз в секунду для анализа данных на лету, поэтому я стараюсь максимально оптимизировать свой код ... -
0@natan: Я думаю, что другие методы на самом деле не «заполняют» всю матрицу нулевыми значениями, а откладывают это до тех пор, пока это не понадобится. Я предполагаю, что MATLAB имеет некоторый внутренний флаг в структуре
mxArrayчтобы указать это состояние. Вот почему само предварительное распределение вводит в заблуждение. Я только добавил более полное сравнение, см. Редактирование ..
После некоторых исследований я нашел эту статью в "Недокументированный Matlab" , в котором Mr. Яир Альтман уже пришел к выводу, что MathWork способ превалирования матриц с использованием zeros(M, N) действительно не самый эффективный способ.
Он приурочил x = zeros(M,N) против clear x, x(M,N) = 0 и обнаружил, что последний примерно в 500 раз быстрее. Согласно его объяснению, второй метод просто создает матрицу M-by-N, элементы которой автоматически инициализируются на 0. Первый метод, однако, создает x (с x с автоматическими нулевыми элементами), а затем назначает нуль для каждого элемента в x снова, и это избыточная операция, которая занимает больше времени.
В случае пустого матричного умножения, такого как то, что вы указали в своем вопросе, MATLAB ожидает, что продукт будет матрицей M × N, и поэтому он выделяет матрицу M × N. Следовательно, выходная матрица автоматически инициализируется нулями. Так как исходные матрицы пустые, дальнейшие вычисления не выполняются, и, следовательно, элементы в выходной матрице остаются неизменными и равными нулю.
-
1Спасибо за обращение к посту Яира Альтмана! для чего это стоит, я также нашел этот FEX-файл mathworks.com/matlabcentral/fileexchange/…, который предполагает оптимизировать предварительное выделение памяти ...
-
0@EitanT +1 за интересный ответ и ссылку на мат. Однако как это объясняет графики, демонстрирующие различное поведение при
n>1000?
Интересный вопрос, видимо, есть несколько способов "избить" встроенную функцию zeros. Мое единственное предположение о том, почему это происходит, было бы в том, что он может быть более эффективным с точки зрения памяти (в конце концов, zeros(LargeNumer) скорее приведет к тому, что Matlab достигнет предела памяти, чем сформирует узкое место в большинстве кодов) или более устойчивым.
Вот еще один метод быстрого выделения, использующий разреженную матрицу, я добавил регулярную нулевую функцию в качестве эталона:
tic; x=zeros(1000,1000); toc
Elapsed time is 0.002863 seconds.
tic; clear x; x(1000,1000)=0; toc
Elapsed time is 0.000282 seconds.
tic; x=full(spalloc(1000,1000,0)); toc
Elapsed time is 0.000273 seconds.
tic; x=spalloc(1000,1000,1000000); toc %Is this the same for practical purposes?
Elapsed time is 0.000281 seconds.
Этот ответ фальсифицирован. Держатся за запись. Кажется, что Matlab решает использовать разреженные матрицы, когда он получил команду как z(n,n)=0; когда n достаточно велико. Внутренняя реализация может быть в виде условия вроде: (если newsize> THRESHOLD + oldsize, то используйте разреженный...), где THRESHOLD является вашим "пороговым размером".
Однако это несмотря на то, что Mathworks утверждает: "Matlab никогда не создает разреженные матрицы автоматически" (ссылка)
У меня нет Matlab, чтобы проверить это. Тем не менее, использование разреженных матриц (внутренне) является более коротким объяснением (бритва Оккама), следовательно, лучше до фальсификации.
Ещё вопросы
- 0JQuery зависимые поля выбора (выбраны)
- 0R или Mysql: изменить значения столбца на ноль, если они отсутствуют в другой строке того же кадра данных
- 1Sphinx - Как сделать autodoc .py файлы, расположенные в нескольких папках?
- 0javascript, div мигает вместо исчезновения
- 0angularjs app.service (…) вызывает «Uncaught TypeError: undefined не является функцией»
- 0UI роутер разрешает проблемы
- 0Как работать с сим-данными по дифференциальным уравнениям
- 0Данные JSON из сервлета в jqGrid не отображаются
- 0on () не сработает, но все остальное работает?
- 1Как заставить Jetty Maven плагин v9.1.x * не * развертывать зависимые военные артефакты?
- 0Проверка формы AngularJS. Невозможно прочитать свойство '$ validators' из неопределенного
- 0Выборка площади против выборки BRDF при рендеринге
- 0Вкладки только рендеринга первой страницы
- 0Форма проверки не работает во время регистрации
- 0Лучше ли всегда проверять возвращаемое значение PDOStatement :: execute?
- 1создать вычтенный фрейм данных, используя несколько значений из нижних строк
- 0Как я могу обновить ту же запись SqlServer внутри цикла sqlsrv_fetch_array?
- 0Почему не работает моя функция printLevel?
- 0Попытка скомпилировать программу winsock в dev C ++ win7 - ошибка
- 1Tomcat Виртуальный хост и Wildcard DNS соответствия
- 0Кнопка «Нравится» / «Рекомендовать» на Facebook не показывает правильную ссылку на лайк или изображение
- 0Как я могу вставить количество в эту корзину php
- 1как связать .so файлы из локального модуля aar в android с файлом приложения android.mk
- 0Эффект аккордеона при наведении мыши с переходами шаток
- 0Освобождение памяти между циклами выполнения
- 0Динамический CSS с AnguarJS / Ionic Framework
- 1Python GUI, который поддерживает интерфейс как CSS & HTML?
- 0Идентификатор возвращает 0 для API отдыха с Go
- 0_DEBUG и LLVM 5.0 C ++: ожидаемое значение препроцессора в выражении
- 0AngularJs - Изменить идентификатор тела или Css с помощью Ng-view
- 0Как использовать функцию PHP crypt () со строкой соли SHA256 для генерации того же хеша, который генерировался бы, если бы SHA256 не поддерживался на сервере?
- 0Почему мой процесс останавливается при запуске в фоновом режиме?
- 0Переадресация со стороны сервера в угловой вид SPA
- 0Предупреждающее сообщение Недопустимый тип смещения от функции Где Mysql php
- 0Ошибка с вызовом oleacc.dll - ошибка доступа запрещена 80020009
- 0Как передать экземпляры класса / структуры в качестве аргументов для обратных вызовов, используя boost :: bind?
- 1Не удается найти сбой символа в тесте Junit
- 1Управляемые событиями веб-приложения на Java?
- 1Как нанести несколько второстепенных сюжетов на фоновое изображение с помощью matplotlib?
- 0Значение столбца не отображается в сетке ng (ui)
- 0вектор push_back не работает
- 0Как использовать список функций, чтобы указать на функцию-член в векторном объекте?
- 0Angular Template Cache - Очистить кэш для обновленного шаблона
- 0MYSQLI - приращение запроса ГДЕ значение за прогон
- 0Абсолютное позиционирование по отношению к родителю
- 0создание элемента jQuery, передача значения
- 1SoftKeyboard накладывается на EditText - ConstraintLayout
- 0Запрос на член не-классового типа
- 0Угловой JS by-src
- 0Ошибки ограничения внешнего ключа
